Artykuły

W poprzednim artykule odkrywaliśmy liczby parzyste, nieparzyste, pierwsze i złożone za pomocą Klocków Cuisenaire’a. Dziś zanurzymy się głębiej w świat liczb, badając dzielniki oraz fascynujące pojęcie rozkładu na czynniki pierwsze. Klocki pozwolą nam wizualizować te abstrakcyjne idee, budując solidne podstawy dla dalszej nauki matematyki. Przyjmijmy, że biały klocek \(\text{BIA} = 1\). Dzielniki liczby Każdą liczbę

W świecie Klocków Cuisenaire’a abstrakcyjne pojęcia matematyczne, takie jak liczby parzyste, nieparzyste i pierwsze, nabierają konkretnego, wizualnego kształtu. Dzięki prostym operacjom na klockach, dzieci mogą samodzielnie odkryć i zdefiniować te terminy, co prowadzi do głębszego i bardziej intuicyjnego zrozumienia. Przyjmijmy, że przyjmujemy, że biały klocek \(\text{BIA} = 1\). Definicje w oparciu o klocki Cuisenaire’a Liczba

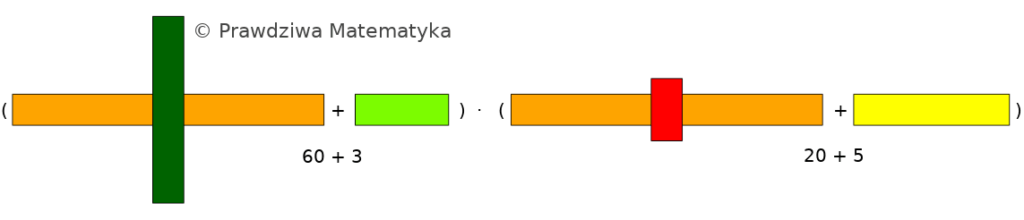
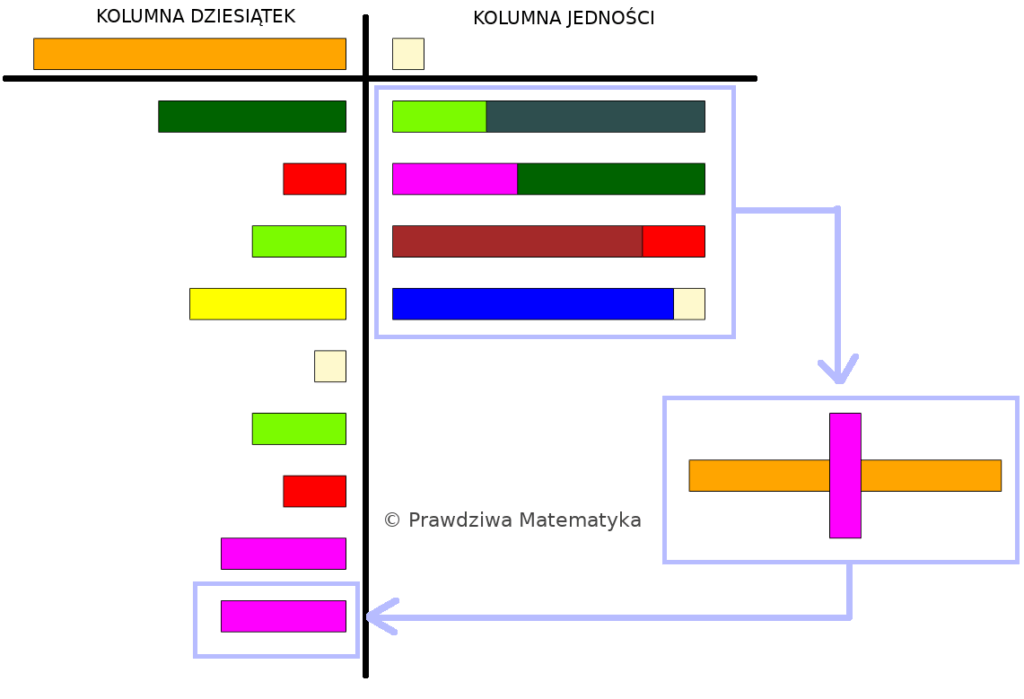
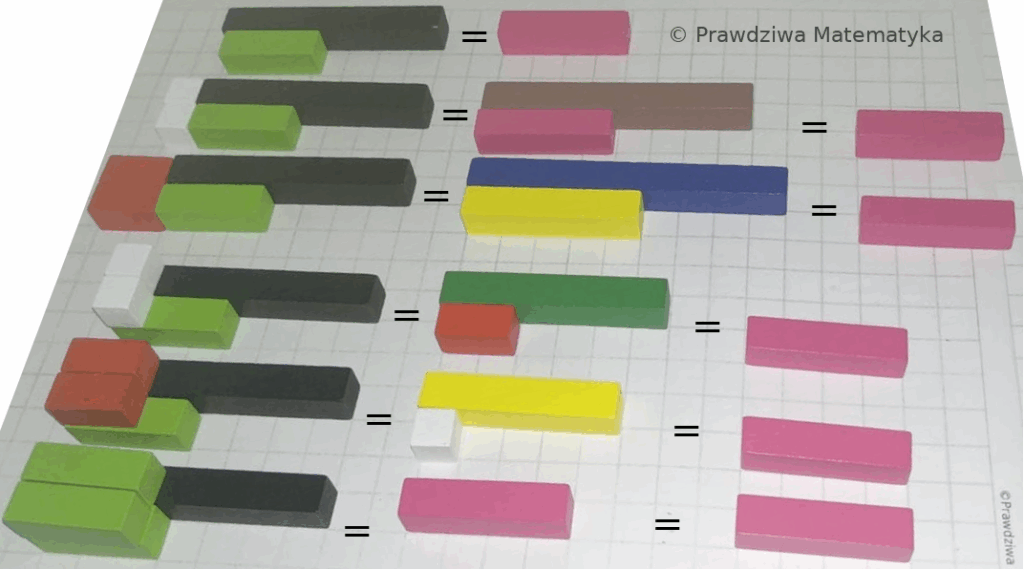
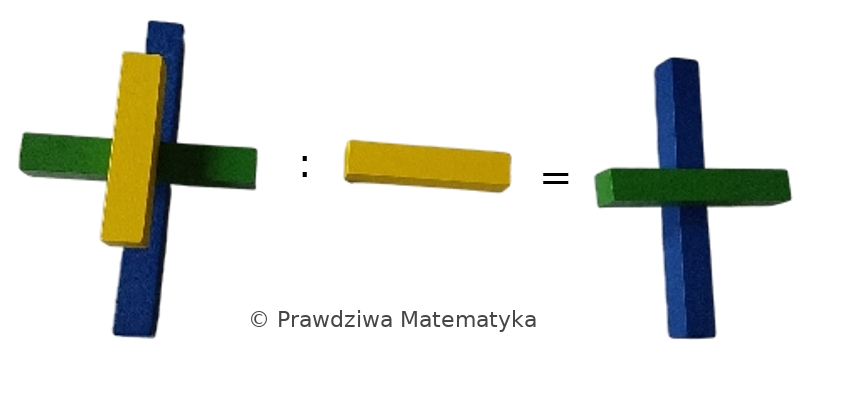
W poprzednim artykule zgłębialiśmy podstawowe zasady mnożenia i jego kluczowe własności, takie jak przemienność, łączność i rozdzielność. Dziś kontynuujemy naszą podróż, skupiając się na praktycznym zastosowaniu prawa rozdzielności w mnożeniu liczb dwucyfrowych – to właśnie tam metoda iloczynów częściowych staje się niezwykle pomocna. Klocki Cuisenaire’a, choć w bardziej zaawansowanych obliczeniach służą głównie do wizualizacji procesu,

Kontynuujemy naszą podróż po świecie arytmetyki z Klockami Cuisenaire’a! Po opanowaniu dodawania i odejmowania, nadszedł czas na mnożenie – operację, która bywa dla wielu dzieci (i dorosłych!) bardziej abstrakcyjna. Klocki Cuisenaire’a oferują jednak konkretny sposób na zrozumienie, czym właściwie jest mnożenie i jak działają jego fundamentalne prawa. Przyjmijmy, że biały klocek (BIA) będzie naszą jednostką

W poprzednich artykułach odkrywaliśmy, jak Klocki Cuisenaire’a pomagają zrozumieć podstawowe operacje dodawania i odejmowania, a także fundamentalne własności tych działań. Dziś idziemy o krok dalej i zmierzymy się z arcyważnymi pojęciami w arytmetyce: ,,przekraczaniem progu” w dodawaniu i ,,rozmienianiem” (potocznie, niezbyt szczęśliwie, nazywanym ,,pożyczaniem”) w odejmowaniu. Klocki Cuisenaire’a sprawią, że te abstrakcyjne mechanizmy staną się

Witajcie w kolejnym artykule z naszej serii o wykorzystywaniu Klocków Cuisenaire’a! Jeśli w poprzednich częściach zafascynowała Was ich moc w rozwijaniu wyobraźni przestrzennej, dziś ponownie zanurzymy się w ich równie niezwykłe zastosowanie w świecie arytmetyki i algebry. To właśnie tutaj klocki stają się mostem łączącym abstrakcyjne pojęcia matematyczne z konkretnym, namacalnym doświadczeniem. Pamiętajcie, że w

Czy matematyka bywa dla Twojego dziecka, a może i dla Ciebie, abstrakcyjnym labiryntem cyfr i symboli? Pamiętasz, jak trudno było zrozumieć, czym właściwie jest \(3 \cdot 5\) albo czym różni się \(\frac{1}{2}\) od \(\frac{2}{4}\)? Na szczęście, Klocki Cuisenaire’a przychodzą z pomocą, oferując konkretne, namacalne narzędzie do wizualizacji podstawowych operacji matematycznych. W naszym poprzednim cyklu artykułów