Artykuły

Klocki Cuisenaire’a a kształtowanie wyobraźni przestrzennej: ,,TANGRAM”

Badania neurologiczne rzucają światło na funkcjonowanie naszego mózgu, wskazując na odrębne funkcje obu półkul. Podczas gdy lewa półkula jest naszym centrum logiki, języka i sekwencyjnego myślenia, to prawa półkula odpowiada za przetwarzanie przestrzenne, percepcyjne i holistyczne. Niestety, nasz system edukacji często nadmiernie koncentruje się na umiejętnościach lewej półkuli, często kosztem rozwoju zdolności przestrzennego rozumowania. Klocki […]

Klocki Cuisenaire’a a kształtowanie wyobraźni przestrzennej: ,,TANGRAM” Dowiedz się więcej »

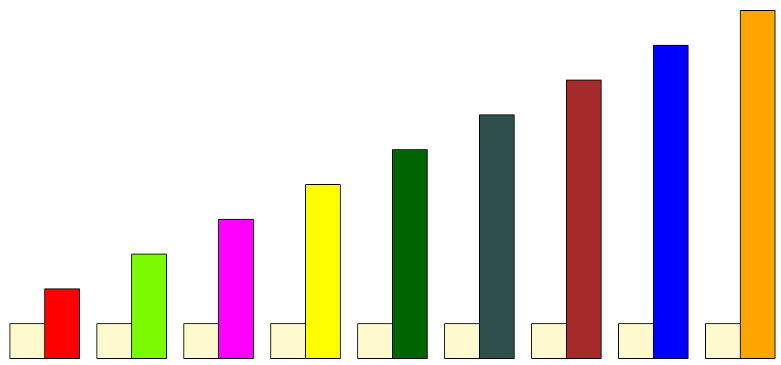
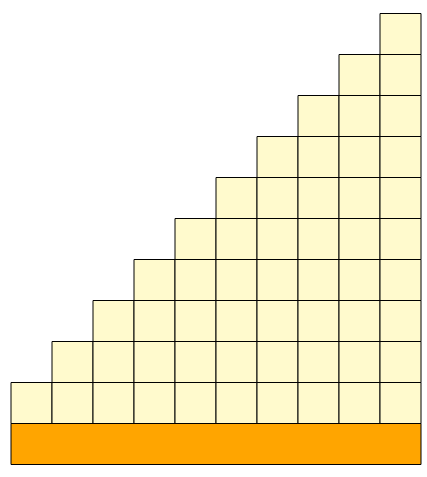
Klocki Cuisenaire’a a relacje między wielkościami

Gdy po raz pierwszy widzimy Klocki Cuisenaire’a, często myślimy: ,,Ale słodkie, to na pewno dla przedszkolaków!” 😀 I owszem, są one fantastyczne dla najmłodszych, pomagając im zrozumieć liczby i podstawy arytmetyki. Ale prawda jest taka, że Klocki Cuisenaire’a to narzędzie, które rewolucjonizuje naukę matematyki na każdym etapie – od przedszkola po wyższe klasy. Dlaczego? Ponieważ,

Klocki Cuisenaire’a a relacje między wielkościami Dowiedz się więcej »

Pierwsze kroki z Klockami Cuisenaire’a

W świecie nauki matematyki, gdzie abstrakcja często bywa wyzwaniem, Klocki Cuisenaire’a jawią się jako oaza konkretu i intuicji. Ale zanim zagłębimy się w szczegółowe lekcje i zaawansowane zastosowania, warto poświęcić czas na… zabawę. Pierwsze spotkanie z tymi kolorowymi klockami powinno być niczym nieskrępowaną, radosną eksploracją 🙂 Zapomnijcie na chwilę o podręcznikach, szczegółowych planach lekcji czy

Pierwsze kroki z Klockami Cuisenaire’a Dowiedz się więcej »

Klocki Cuisenaire’a – poznaj pomoc, która ułatwia naukę matematyki!

Zastanawiasz się, jak w prosty i angażujący sposób pomóc dziecku zrozumieć matematykę? Klocki Cuisenaire’a to świetne narzędzie, które od lat wspiera nauczycieli i rodziców w nauczaniu podstawowych pojęć matematycznych. Ale czym właściwie są te kolorowe patyczki? Klocki Cuisenaire’a to zestaw drewnianych lub plastikowych prostopadłościenny klocków o różnych długościach i kolorach. Najkrótszy klocek ma długość 1

Klocki Cuisenaire’a – poznaj pomoc, która ułatwia naukę matematyki! Dowiedz się więcej »

Matematyka zaczyna się wcześniej, niż myślisz!

Zastanawiasz się, czy Twoje dziecko przejawia oznaki rozwoju umiejętności matematycznych, ale nie wiesz, jak je rozpoznać? A może odnosisz wrażenie, że Twoje dziecko rozwija się nieharmonijnie i martwisz się, że mimo młodego wieku jest “do tyłu” z matematyką? Myślenie matematyczne zaczyna rozwijać się wcześniej, a jego przejawy są bardziej subtelne, niż mogłoby się wydawać, dlatego zdarza się,

Matematyka zaczyna się wcześniej, niż myślisz! Dowiedz się więcej »

Matematyka a praktyka

Uczniowie, mimo znajomości wzorów i procedur, często mają trudności z ich zastosowaniem w praktycznych sytuacjach. W tym wpisie poruszę istotny aspekt nauczania matematyki, który często jest pomijany, a mianowicie umiejętność stosowania wiedzy matematycznej w konkretnych kontekstach. Trzy aspekty edukacji matematycznej W poprzednich wpisach omówiłam dwa kluczowe aspekty edukacji matematyki: logiczne podstawy pojęć oraz konwencje kulturowe,

Matematyka a praktyka Dowiedz się więcej »

Matematyka a konwencje kulturowe

Jako nauczycielka matematyki z wieloletnim doświadczeniem, pragnę zwrócić Waszą uwagę na ważny aspekt edukacji matematycznej, który często jest pomijany. Choć logika jest fundamentem tej dziedziny, to bardzo istotne są konwencje, czyli kulturowe narzędzia, które ułatwiają zrozumienie i stosowanie matematycznych koncepcji. Uczenie dzieci matematyki to nie tylko przekazywanie im rządzących nią reguł, ale także wprowadzanie ich w

Matematyka a konwencje kulturowe Dowiedz się więcej »

Matematyka a logika

Matematyka nie jest tylko przedmiotem, który wymaga opanowania zestawu procedur – jest to dziedzina, w której zrozumienie logicznych zasad jest fundamentem skutecznego uczenia się. Jako nauczycielka matematyki z wieloletnim doświadczeniem, przekonałam się, że najważniejszym celem w nauce matematyki jest rozwijanie zdolności myślenia logicznego u uczniów. To właśnie logika stanowi podstawę każdej matematycznej operacji, nawet tej

Matematyka a logika Dowiedz się więcej »

Kiedy liczba jest podzielna przez 13? Regułka kontra zrozumienie

Wyobraź sobie, że jesteś w szkole na lekcji matematyki i uczysz się nowej regułki matematycznej, a konkretnie – jak sprawdzić, czy dana liczba jest podzielna przez 13. Oto procedura, którą nauczyciel każe Ci zapamiętać: Spróbujmy to na przykładzie. Czy liczba 45238 jest podzielna przez 13? Liczba 45238 nie jest podzielna przez 13. Proste, prawda? Teraz

Kiedy liczba jest podzielna przez 13? Regułka kontra zrozumienie Dowiedz się więcej »

Kryteria oceny i ich zastosowanie w matematyce (cz.III)

Samoocena z wykorzystaniem kryteriów oceny – jak to wygląda w praktyce? Kiedy rozpoczynam współpracę z nową grupą, na samym początku omawiam z dziećmi kryteria oceny, które będę stosowała na zajęciach. Omawiam je z uczniami i od razu tłumaczę, że oceny będą częściej związane z tym, jak dobrze rozumieją i rozwiązują zadania, a nie tylko z liczbą

Kryteria oceny i ich zastosowanie w matematyce (cz.III) Dowiedz się więcej »

Przewijanie do góry