Kurs Prawdziwej Matematyki dla 5. klasy

Twoje dziecko uczy się krok po kroku w zrozumiały sposób

178 lekcji

Cała podstawa programowa
zrealizowana w krótkich,
przystępnych nagraniach

Bieżące
wsparcie

2x w tygodniu spotkania online
z dyżurującym nauczycielem
(rozwiej na bieżąco wszystkie wątpliwości)

Opcja Premium

1x w tygodniu grupowa lekcja online prowadzona na żywo przez nauczyciela
(Pakiet Premium)

Opcja Live

Możliwość dołączenia do grupowych lekcji na żywo, bez wykupywania dostępu do nagrań i materiałów
(Pakiet Live)

Zapisz swoje dziecko na unikalny kurs matematyki, który w piątej klasie nadal stawia na głębokie zrozumienie i praktyczne podejście do nauki.

Naszym celem nie jest “odhaczenie” podstawy programowej, ale prawdziwe, gruntowne opanowanie zagadnień, które pozwoli Twojemu dziecku na znaczący rozwój umiejętności samodzielnego myślenia matematycznego. Dzięki temu zyska solidne fundamenty pod dalszą naukę!

Kurs składa się z krótkich, efektywnych lekcji (około 45-50 minut). Dzięki temu Twoje dziecko będzie poznawało kolejne, bardziej zaawansowane zagadnienia stopniowo i dokładnie, a Ty zyskasz pewność, że kompleksowo rozwija swoje umiejętności na tym etapie edukacji.

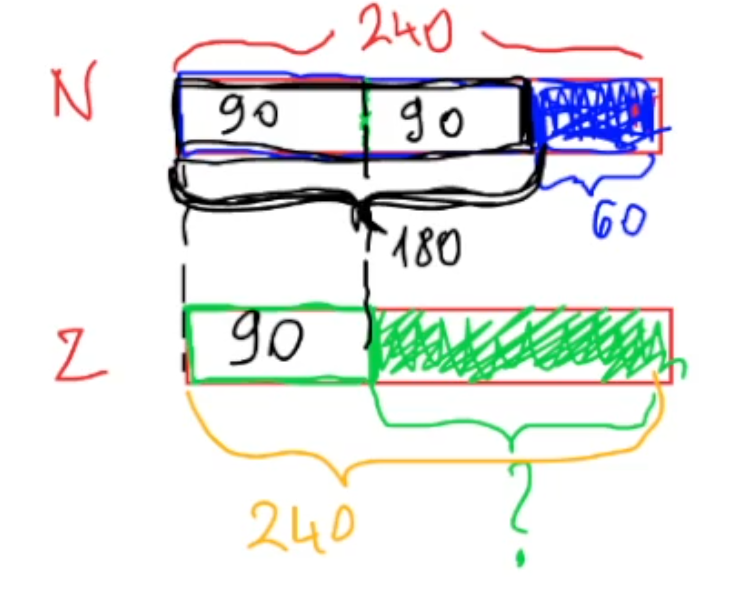
Uczniowie pracują z wykorzystaniem różnorodnych pomocy dydaktycznych, dzięki czemu matematyka staje się mniej abstrakcyjna, a bardziej namacalna i zrozumiała. W trakcie kursu dzieci ilustrują treść zadań za pomocą różnych modeli, co znacząco ułatwia im opanowanie i rozwiązywanie nawet bardzo skomplikowanych problemów.

Oprócz poznawania nowych, bardziej złożonych tematów, kurs kładzie szczególny nacisk na rozwijanie intuicji matematycznej oraz wzmacnianie rozumienia działania i regularności systemu liczbowego.

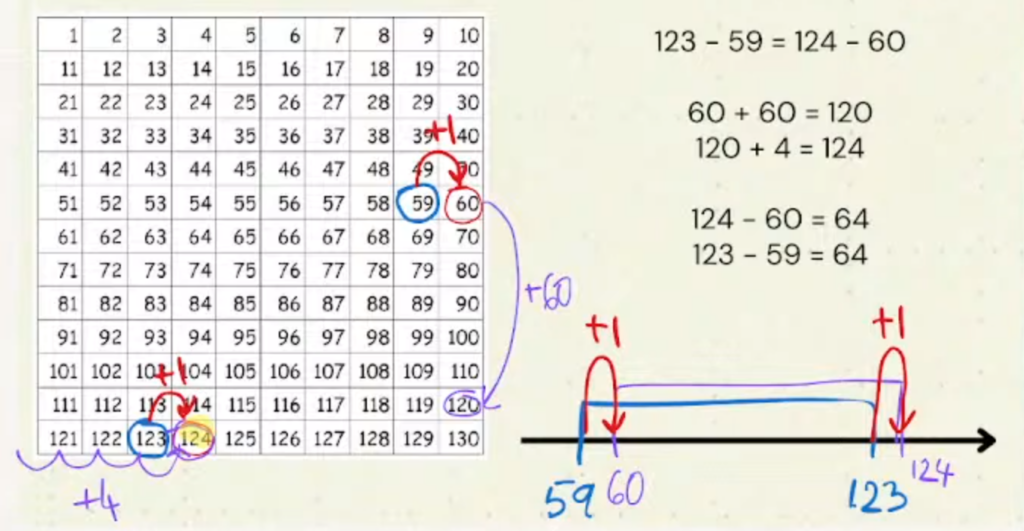
Obok tradycyjnych algorytmów wymaganych w podstawie programowej, dzieci poznają wiele strategii efektywnego (czyli sprytnego) wykonywania obliczeń, co rozwija ich elastyczność w myśleniu matematycznym.

Zofia Zielińska-Kolasińska

Z wykształcenia matematyk, z pasji edukator.

Ponad 20 lat doświadczenia w pracy z dziećmi, młodzieżą i dorosłymi.

Nie uznaję kompromisów w nauczaniu matematyki — albo zrozumienie, albo nic.

Wierzę, że to nauczyciel ma tak poprowadzić ucznia, by zrozumiał, a nie tylko zapamiętał.

Bo matematyka to nie regułki – to sposób myślenia.

Chcesz wiedzieć o mnie więcej? Kliknij w moje zdjęcie!

Wszyscy uczniowie zapisani na Kurs otrzymują bieżące wsparcie nauczyciela, który dyżuruje w ustalonych terminach.

Można połączyć się z nim na rozmowę na żywo lub wysłać wiadomość z prośbą o pomoc.

Kurs w budowie:
Obecnie dostępne są już pierwsze moduły kursu, a do września planujemy udostępnić kolejne, aby Twoje dziecko mogło płynnie rozpocząć naukę. Pozostałe moduły będą sukcesywnie dodawane w trakcie roku szkolnego.

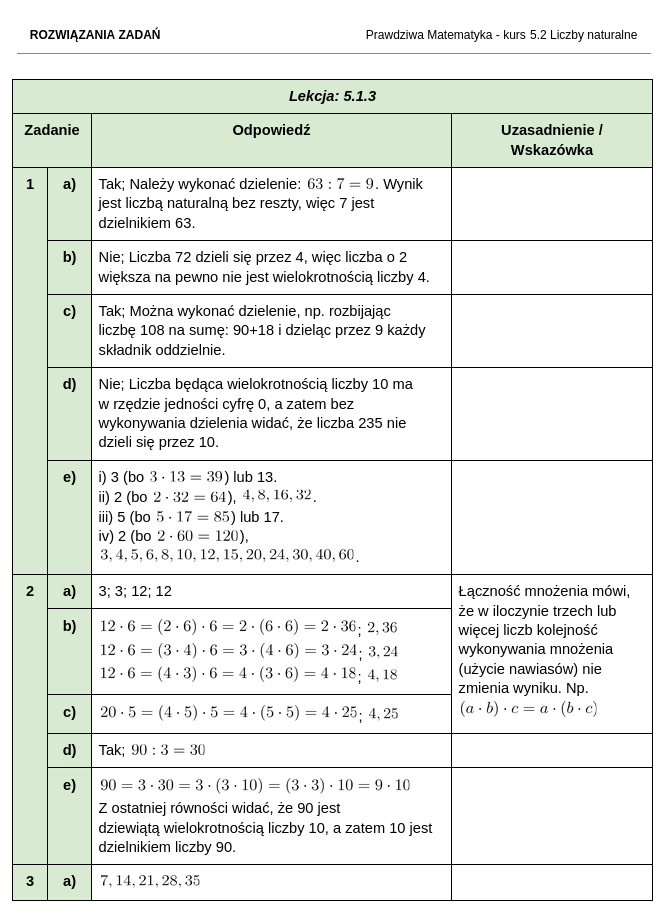
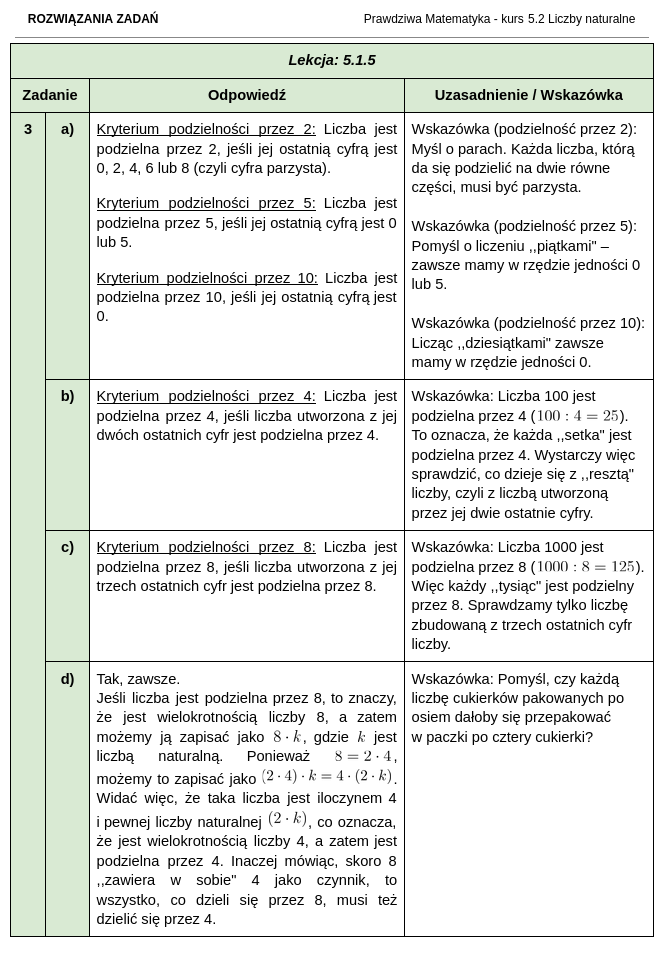
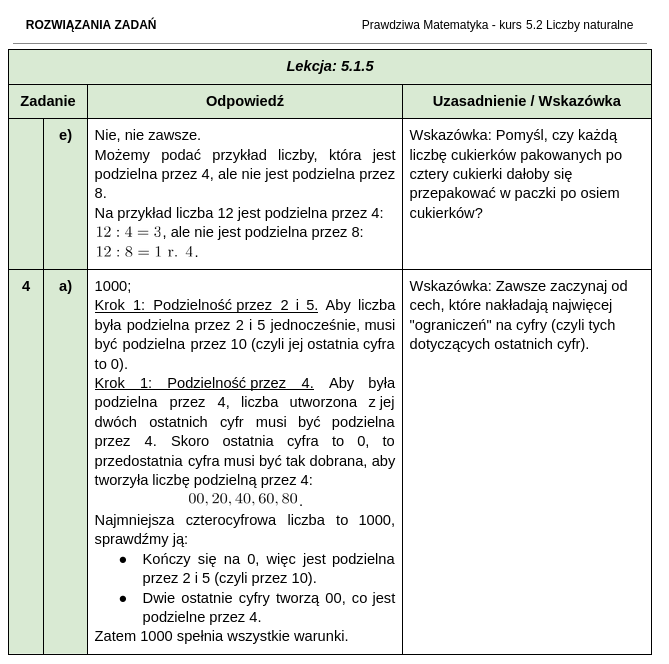
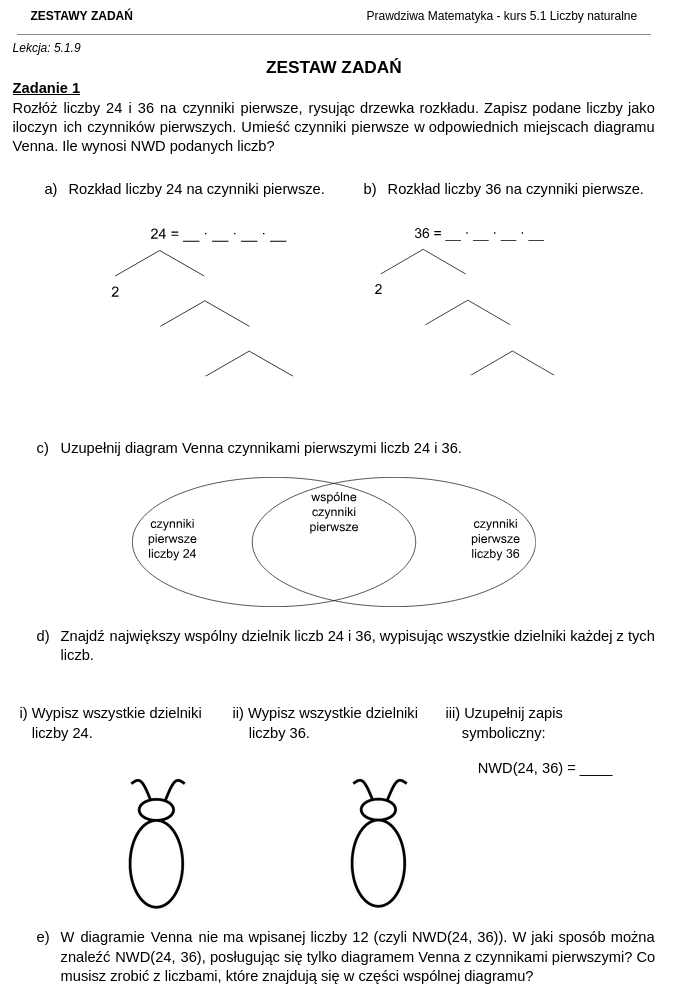
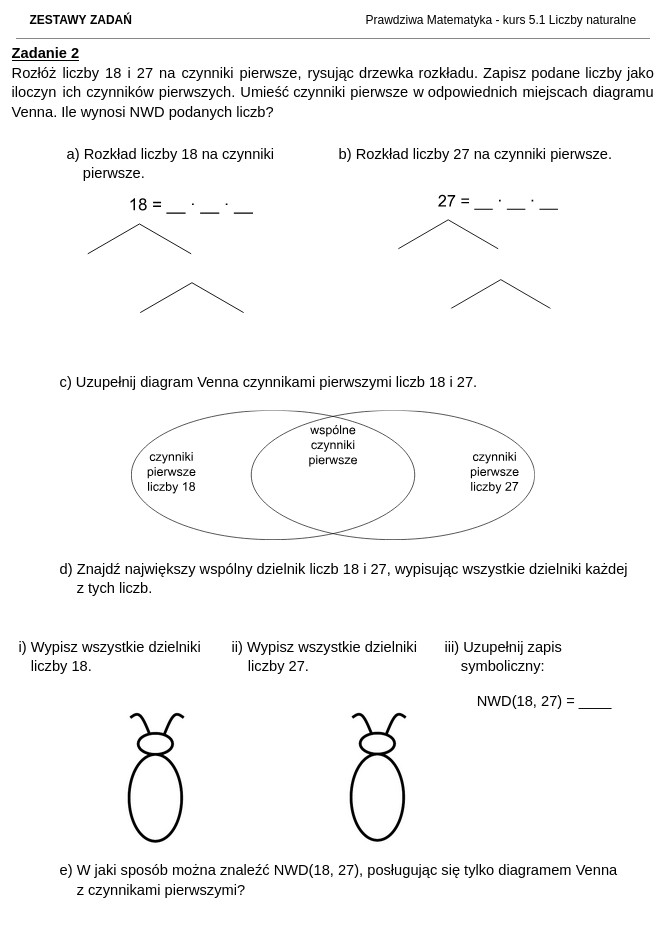
Jak wyglądają nagrane ćwiczenia?

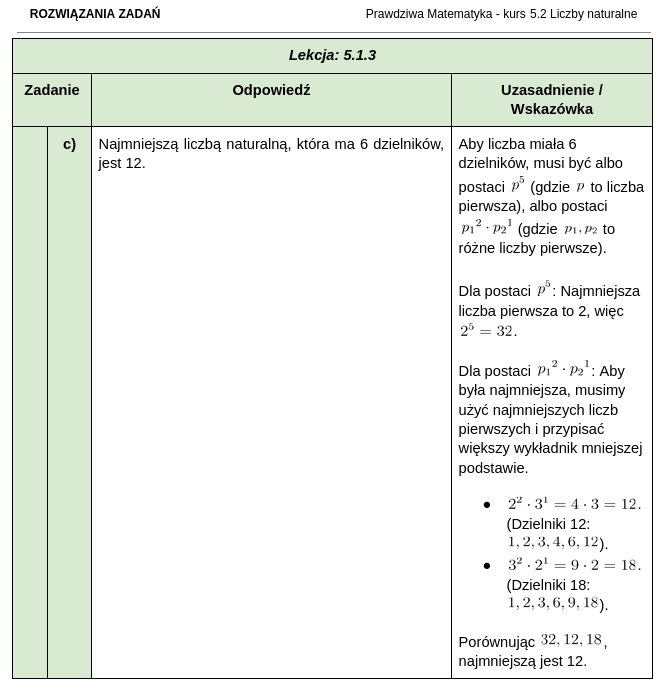
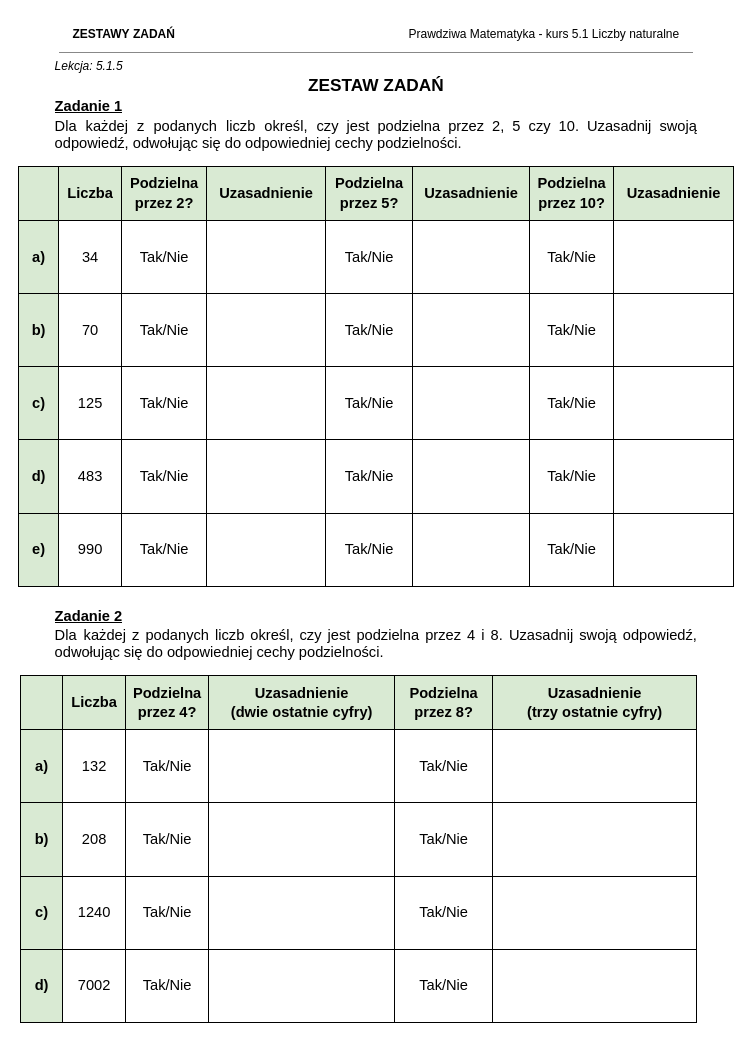
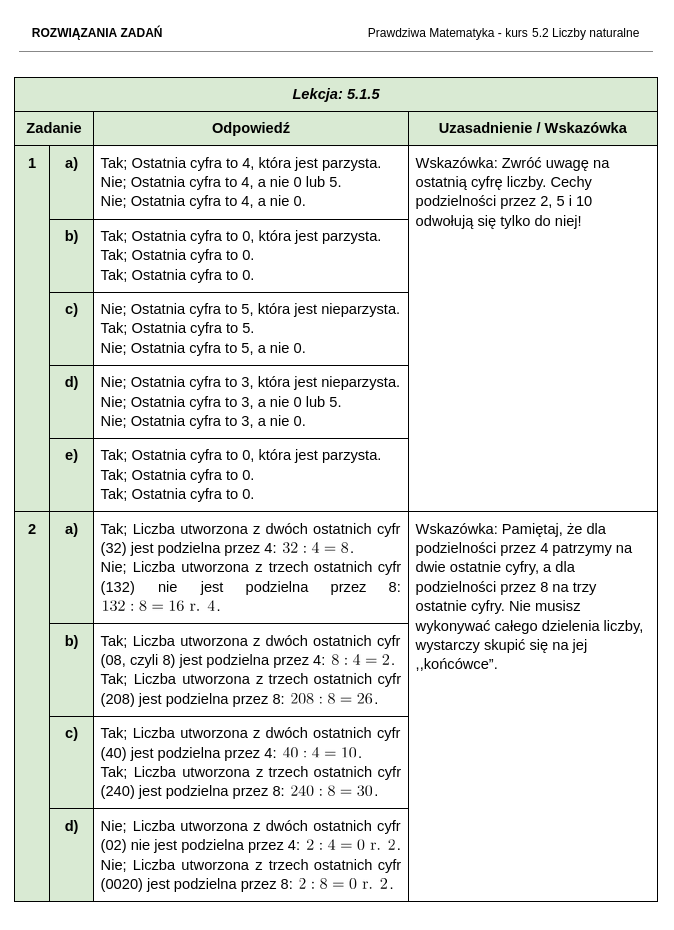
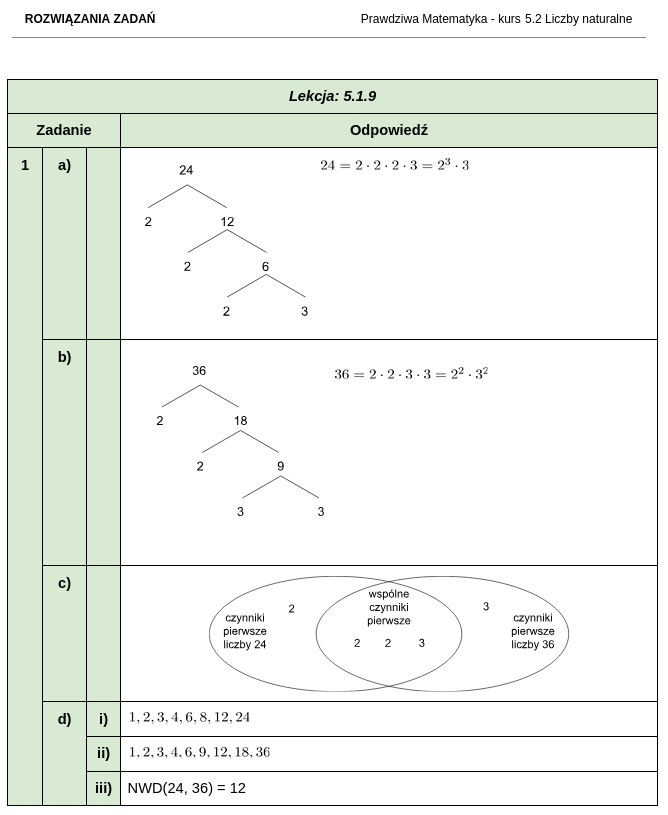
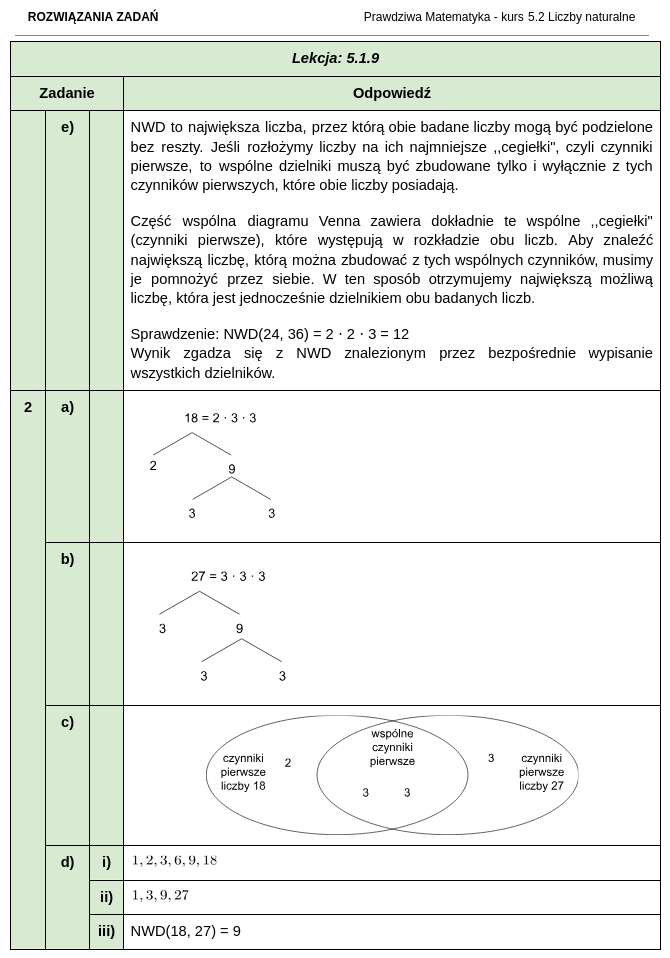
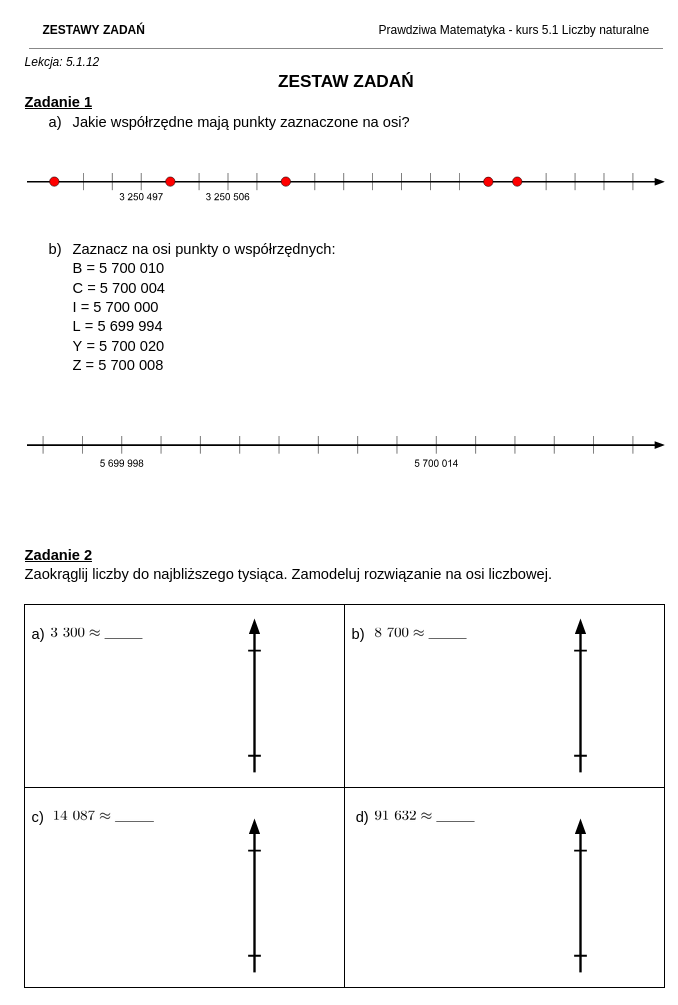
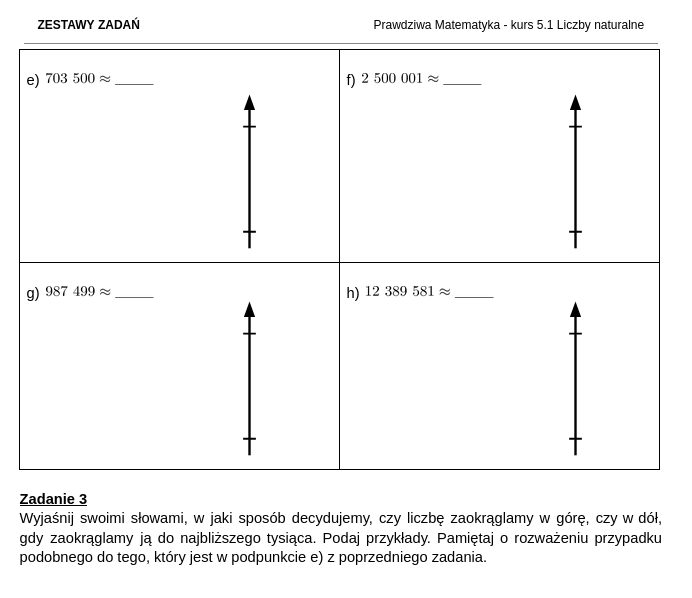
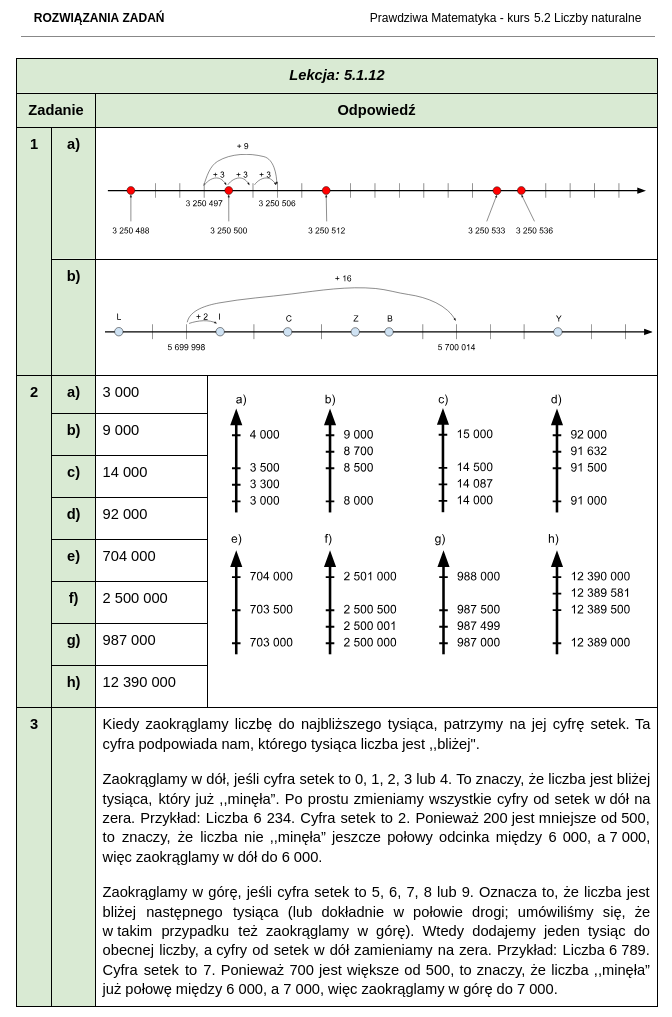
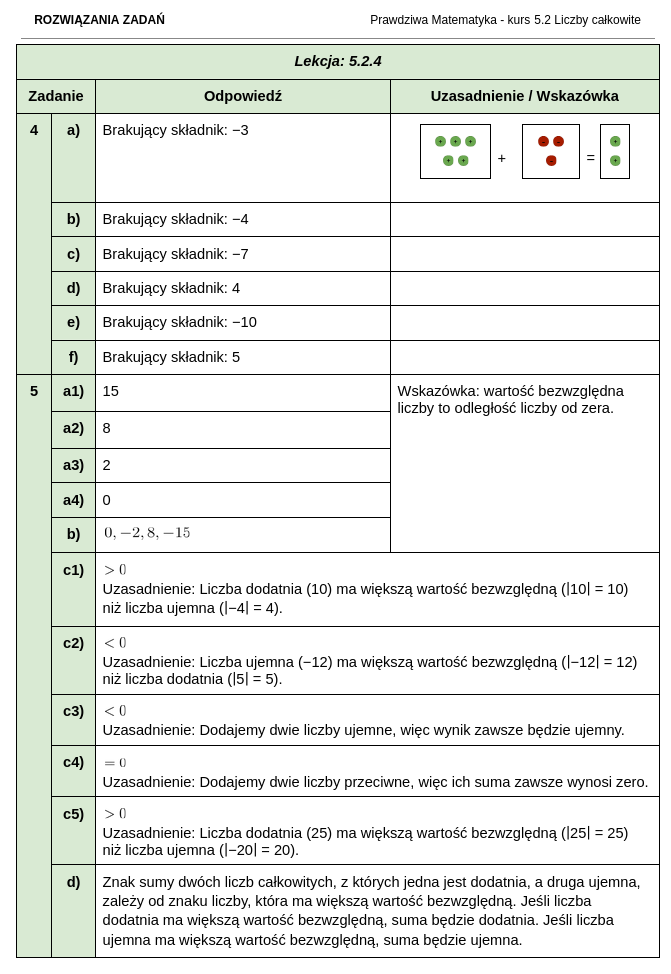
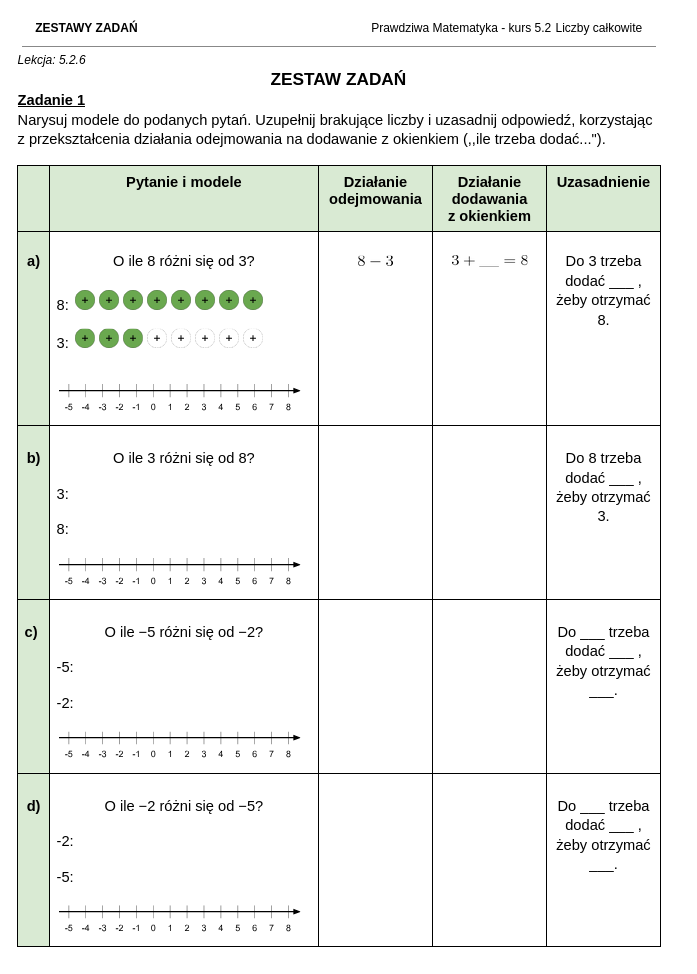
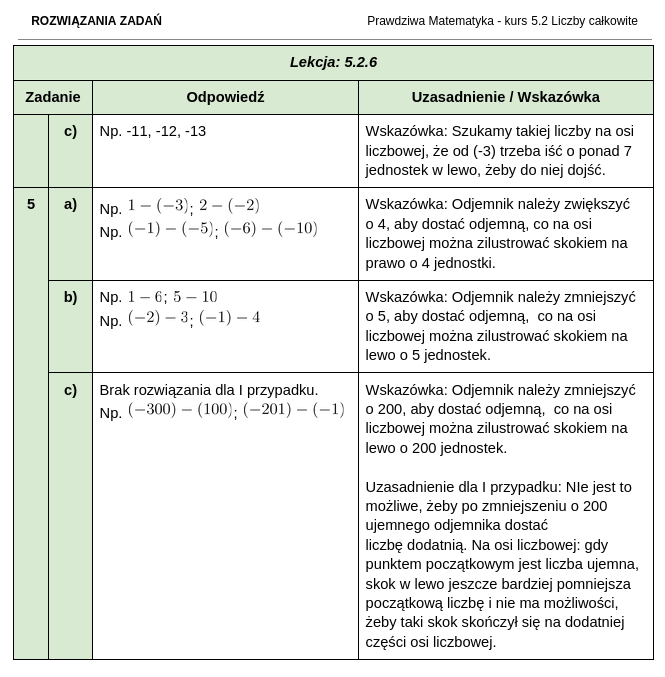
Jak wyglądają zestawy zadań i rozwiązania?

Z jakich modułów składa się Kurs?

W skład Kursu wchodzi 11 modułów.

W tym module uczniowie będą:

  • Rozpoznawać i klasyfikować liczby:
    • Rozróżniać liczby parzyste i nieparzyste.
    • Definiować i identyfikować liczby pierwsze i złożone.
  • Działać z dzielnikami i wielokrotnościami liczb:
    • Sprawnie znajdować dzielniki liczb.
    • Znajdować dzielniki liczb w oparciu o łączność mnożenia.
    • Określać wielokrotności liczb.
  • Stosować metodę sita:
    • Wykorzystywać Sito Eratostenesa do znajdowania liczb pierwszych.
  • Poznawać cechy podzielności liczb:
    • Rozpoznawać podzielność liczb przez 2, 3, 4, 5, 8, 9 i 10.
  • Obliczać NWD i NWW liczb:
    • Definiować i wyznaczać Największy Wspólny Dzielnik (NWD).
    • Definiować i wyznaczać Najmniejszą Wspólną Wielokrotność (NWW).
  • Rozkładać liczby na czynniki pierwsze:
    • Znajdować rozkład liczby na czynniki pierwsze.
    • Stosować rozkład na czynniki pierwsze do wyłączania NWD przed nawias.
  • Poznawać Algorytm Euklidesa:
    • Wykorzystywać Algorytm Euklidesa do wyznaczania NWD.
  • Zaokrąglać liczby naturalne:
    • Zaznaczać i odczytywać liczby naturalne na osi liczbowej.
    • Zaokrąglać liczby naturalne do dowolnego miejsca (np. do dziesiątek, setek, tysięcy).
    • Stosować zaokrąglanie liczb naturalnych w problemach życia codziennego.

W tym module uczniowie będą:

  • Poznawać liczby całkowite:
    • Rozróżniać i definiować liczby dodatnie i ujemne.
    • Umieszczać i interpretować liczby dodatnie i ujemne na osi liczbowej.
    • Rozumieć liczby całkowite w praktycznym kontekście (np. finanse, temperatura, wysokość n.p.m.).
    • Definiować i znajdować liczbę przeciwną oraz rozumieć pojęcie “przeciwna do przeciwnej”.
  • Wykonywać działania na liczbach całkowitych:
    • Dodawać liczby całkowite.
    • Rozumieć odejmowanie liczb całkowitych zarówno jako “zabieranie”, jak i “różnicę”.
    • Mnożyć liczby całkowite.
    • Dzielić liczby całkowite.

W tym module uczniowie będą:

  • Poznawać i budować zrozumienie liczb dziesiętnych:
    • Interpretować liczby dziesiętne w tabeli rzędów wielkości.
    • Rozpoznawać różne sposoby zapisu liczby dziesiętnej.
    • Umieszczać liczby dziesiętne na osi liczbowej.
    • Porównywać liczby dziesiętne.
  • Wykonywać działania z potęgami liczby 10:
    • Mnożyć i dzielić liczby dziesiętne przez potęgi liczby 10.
    • Stosować te działania w kontekście przeliczania jednostek długości (m ↔ cm ↔ mm).
  • Zaokrąglać liczby dziesiętne:
    • Zaokrąglać liczby dziesiętne do dowolnego miejsca, również z wykorzystaniem osi liczbowej.
  • Wykonywać podstawowe działania na liczbach dziesiętnych:
    • Dodawać i odejmować liczby dziesiętne.
    • Mnożyć liczby dziesiętne przez jednocyfrowe liczby naturalne (w tym modelowanie mnożenia).
    • Dzielić liczby dziesiętne przez jednocyfrowe liczby naturalne (z wykorzystaniem jednostek i tabeli rzędów wielkości).
  • Stosować wiedzę w praktyce:
    • Rozpoznawać i wykorzystywać praktyczne zastosowania działań na liczbach dziesiętnych w życiu codziennym.

W tym module uczniowie będą:

  • Budować podstawy dotyczące mnożenia liczb naturalnych:
    • Wprowadzać się w koncepcję mnożenia.
    • Obliczać iloczyny dwucyfrowych wielokrotności liczby 10.
    • Mnożyć liczby naturalne przez wielokrotności liczby 10.
    • Szacować wartości iloczynów liczb naturalnych.
    • Interpretować mnożenie jako wielokrotne dodawanie.
  • Posługiwać się tradycyjnym algorytmem mnożenia:
    • Stosować tradycyjny algorytm mnożenia liczb naturalnych, zarówno dla 2, jak i dla 4 i więcej iloczynów częściowych.
    • Poznawać praktyczne zastosowania tego algorytmu.
  • Mnożyć liczby dziesiętne:
    • Mnożyć liczby dziesiętne w postaci z jednostkami (części dziesiąte i setne).
  • Przeliczać jednostki:
    • Dokonywać przeliczania jednostek poprzez mnożenie przez liczbę naturalną.
    • Przeliczać jednostki poprzez mnożenie przez liczbę dziesiętną lub ułamek.
    • Poznawać praktyczne zastosowania przeliczania jednostek w codziennym życiu.
  • Zapisywać i porównywać wyrażenia algebraiczne:
    • Poznawać kolejność wykonywania działań w wyrażeniach.

W tym module uczniowie będą:

  • Poznawać podstawy dzielenia liczb naturalnych:
    • Wprowadzać się w koncepcję dzielenia.
    • Stosować schemat dzielenia przez potęgi liczby 10 dla liczb naturalnych.
    • Szacować wartości ilorazów liczb naturalnych.
  • Dzielić liczby naturalne:
    • Używać tradycyjnego algorytmu dzielenia liczb naturalnych.
    • Wykonywać dzielenie z resztą liczb naturalnych (przez wielokrotność liczby 10 oraz gdy iloraz jest jednocyfrowy).
  • Dzielić liczby dziesiętne:
    • Dzielić liczby dziesiętne przez liczby naturalne.
    • Wykonywać dzielenie z resztą liczb dziesiętnych przez wielokrotność liczby 10.
    • Szacować rząd wielkości ilorazu i poprawnie umieszczać przecinek dziesiętny.
    • Dzielić liczbę dziesiętną przez dwucyfrowy dzielnik.
  • Stosować różne typy dzielenia w praktyce:
    • Rozpoznawać i wykorzystywać dwa typy dzielenia w praktyce: dzielenie typu “na” oraz dzielenie typu “po”.

W tym module uczniowie będą:

  • Poznawać i porównywać ułamki:
    • Modelować ułamki równoważne na różne sposoby.
    • Umieszczać ułamki i liczby mieszane na osi liczbowej.
    • Porównywać ułamki, w tym do punktów odniesienia (np. \(1\over2\), \(2\), \(1\)\(1\over2\)) oraz poprzez sprowadzanie do wspólnego mianownika.
    • Rozumieć relację części do całości.
  • Wykonywać dodawanie i odejmowanie ułamków:
    • Rozbijać ułamek na sumę ułamków.
    • Modelować dodawanie i odejmowanie ułamków o różnych mianownikach.
    • Dodawać ułamki (również te, których suma jest większa niż 1 i mniejsza od 2) oraz liczby mieszane (sumy większe niż 2), w tym sprowadzając do wspólnego mianownika bez modelowania.
    • Odejmować ułamki od liczb większych od 1 i mniejszych od 2, a także odejmować ułamki i liczby mieszane (w tym sprowadzając do wspólnego mianownika bez modelowania).
    • Dodawać i odejmować ułamki i liczby mieszane od liczb naturalnych.
  • Stosować strategie rozwiązywania problemów:
    • Szacować wyniki dodawania i odejmowania ułamków.
    • Wykonywać działania wieloskładnikowe na ułamkach.
    • Rozpoznawać i wykorzystywać praktyczne zastosowania dodawania i odejmowania ułamków zwykłych i liczb mieszanych.

W tym module uczniowie będą:

  • Obliczać iloczyn ułamka przez liczbę naturalną:
    • Interpretować ułamek jako wynik dzielenia.
    • Określać ułamek zbioru lub liczby.
    • Mnożyć liczbę naturalną przez ułamek (poprzez wielokrotne dodawanie).
    • Stosować kolejność wykonywania działań w kontekście ułamków zwykłych.
    • Wykorzystywać praktyczne zastosowania obliczania iloczynu ułamka przez liczbę naturalną.
  • Obliczać iloczyn ułamka przez ułamek:
    • Mnożyć ułamek jednostkowy przez ułamek jednostkowy.
    • Mnożyć ułamek jednostkowy przez ułamek niejednostkowy.
    • Mnożyć ułamek niejednostkowy przez ułamek niejednostkowy.
    • Poznawać praktyczne zastosowania obliczania iloczynu ułamka przez ułamek.
  • Porównywać mnożenie ułamków zwykłych i dziesiętnych:
    • Łączyć koncepcję mnożenia ułamków zwykłych z mnożeniem ułamków dziesiętnych.
    • Obliczać iloczyny ułamków zwykłych i dziesiętnych w kontekście miar.
  • Analizować efekty mnożenia:
    • Postrzegać mnożenie jako skalowanie.
    • Rozważać mnożenie przez 1 w kontekście ułamków równoważnych.
    • Analizować wielkość iloczynu w odniesieniu do wielkości czynników.
    • Wykorzystywać praktyczne zastosowania obliczania iloczynu przez ułamek zwykły lub dziesiętny.

W tym module uczniowie będą:

  • Wykonywać dzielenie ułamków zwykłych:
    • Dzielić liczbę naturalną przez ułamek jednostkowy (interpretacja “po”).
    • Dzielić ułamek jednostkowy przez liczbę naturalną (interpretacja “na”).
    • Układać działania i zadania z treścią na podstawie modeli paskowych.
    • Przechodzić od dzielenia przez ułamek do mnożenia przez jego odwrotność.
    • Dzielić ułamki i liczby mieszane.
    • Stosować praktyczne zastosowania obliczania ilorazu liczby naturalnej przez ułamek jednostkowy oraz ułamka jednostkowego przez liczbę naturalną.
  • Wykonywać dzielenie ułamków dziesiętnych oraz liczb dziesiętnych:
    • Dzielić przez ułamek jednostkowy (w tym dzielenie przez \(0{,}1\) i \(0{,}01\)).
    • Dzielić liczby dziesiętne przez niejednostkowe ułamki dziesiętne.
  • Wprowadzać się w zagadnienia uzupełniające:
    • Zapisywać wyrażenia algebraiczne.
    • Wykorzystywać praktyczne zastosowania mnożenia i dzielenia ułamków zwykłych i dziesiętnych.
  • Poznawać procenty:
    • Definiować i obliczać procenty.

W tym module uczniowie będą:

  • Poznawać podstawowe pojęcia geometryczne:
    • Identyfikować punkt, prostą, półprostą i kąt.
    • Rozróżniać rodzaje kątów (np. ostre, proste, rozwarte, pełne).
    • Wyznaczać proste prostopadłe i równoległe.
    • Poznawać miarę 1 stopnia oraz wielokrotności kąta prostego.
    • Zauważać, że taki sam kąt zachowuje miarę niezależnie od wielkości okręgu.
    • Mierzyć i rysować kąty.
    • Obliczać nieznaną miarę kąta, wykorzystując wiedzę o kątach przyległych i wierzchołkowych.
    • Rozpoznawać kąty odpowiadające i naprzemianległe.
    • Definiować łamaną i wielokąt oraz obliczać obwód wielokąta.
    • Poznawać pojęcie symetrii.
  • Posługiwać się skalą:
    • Stosować skalę w praktyce, w tym na planie i mapie.
  • Klasyfikować i konstruować trójkąty oraz czworokąty:
    • Klasyfikować rodzaje trójkątów (np. równoboczne, równoramienne, różnoboczne, prostokątne).
    • Konstruować trójkąty spełniające podane warunki.
    • Klasyfikować czworokąty, w tym trapezy, równoległoboki, romby, prostokąty i deltoidy.
    • Rysować czworokąty o podanych cechach.

W tym module uczniowie będą:

  • Wyznaczać pole powierzchni prostokąta:
    • Znajdować pole powierzchni prostokąta poprzez kafelkowanie.
    • Obliczać pole powierzchni prostokąta za pomocą wzoru.
    • Łączyć iloczyn liczb mieszanych z modelem pola prostokąta.
    • Stosować praktyczne zastosowania obliczania pola powierzchni prostokąta.
  • Obliczać pole powierzchni innych figur płaskich:
    • Obliczać pole powierzchni równoległoboku.
    • Obliczać pole powierzchni trójkąta prostokątnego.
    • Obliczać pole powierzchni trójkąta ostrokątnego.
    • Obliczać pole powierzchni dowolnego trójkąta.
    • Obliczać pola powierzchni nieregularnych figur płaskich poprzez rozcinanie (np. trapezu).
    • Wykorzystywać praktyczne zastosowania obliczania pól powierzchni figur płaskich.
  • Poznawać zależności między jednostkami pola:
    • Operować jednostkami cm\(^2\), mm\(^2\), dm\(^2\).
    • Posługiwać się jednostkami m\(^2\), a (ary), ha (hektary).

W tym module uczniowie będą:

  • Poznawać podstawowe cechy brył:
    • Identyfikować wierzchołki, krawędzie i ściany brył.
    • Rysować siatki sześcianu i prostopadłościanu.
  • Obliczać pole powierzchni prostopadłościanu:
    • Wyznaczać pole powierzchni prostopadłościanu.
  • Wprowadzać się w pojęcie objętości:
    • Określać, czym jest objętość.
    • Sprawdzać, ile sześcianów jednostkowych zmieści się w prostopadłościanie.
    • Rozkładać prostopadłościan na warstwy w celu zrozumienia objętości.
  • Obliczać objętość prostopadłościanu:
    • Obliczać objętość prostopadłościanu poprzez mnożenie długości krawędzi.
    • Wyrażać objętość w jednostkach sześciennych i w litrach.
    • Obliczać łączną objętość zestawu prostopadłościanów.
    • Wykorzystywać praktyczne zastosowania obliczania objętości.

Co wchodzi w skład pojedynczego modułu?

Pozwala sprawdzić przed zakupem, czy uczeń opanował już materiał danego modułu.

Każda lekcja składa się z:

  • rozgrzewki (jeden lub kilka quizów powtórzeniowych)
  • ćwiczeń w formie nagranych filmików
  • zestawu zadań do wydrukowania i samodzielnego rozwiązania
  • rozwiązań zadań

Niektóre tematy zawierają dodatkowo materiały do druku.

Powtórzenie materiału z całego modułu w formie nagranych ćwiczeń oraz sprawdzian do samodzielnego rozwiązania.

Ile kosztuje udział w Kursie?

Cena Kursu: 3 204 zł

cena pakietu standard + 50 zł za każdą lekcję grupową*

100 zł za każdą lekcję grupową*

* Płatność za lekcje grupowe pobierana jest z góry za 4 kolejne spotkania.

Ceny poszczególnych modułów obliczane są proporcjonalnie do liczby tematów w module.

ModułLiczba lekcjiCena modułu
Moduł 116288 zł
Moduł 210180 zł
Moduł 316288 zł
Moduł 415270 zł
Moduł 513234 zł
Moduł 623414 zł
Moduł 719342 zł
Moduł 815270 zł
Moduł 922396 zł
Moduł 1015270 zł
Moduł 1114252 zł
ŁĄCZNIE1783 204 zł

Jak zapisać dziecko na Kurs?

Zakup modułów możliwy jest w Sklepie. Kolejne moduły wymagają jeszcze “doszlifowania”, więc będą pojawiały się w Sklepie sukcesywnie.

Jeżeli są Państwo zainteresowani udziałem dziecka w zajęciach na żywo (pakiet Premium lub Live), zapraszam do zarezerwowania miejsca w grupie poprzez wypełnienie FORMULARZA. Liczba miejsc jest ograniczona.

O czym pamiętać zapisując dziecko na Kurs?

Kurs podzielony jest na 11 modułów, z których każdy można wykupić osobno.

Zachęcam do rozpoczynania nauki od Modułu 1 i kontynuowania po kolei aż do Modułu 11. Dzięki temu uczeń zyska pełny, logiczny obraz materiału i zrealizuje całą podstawę programową w przemyślanej, uporządkowanej formie.

Kurs w budowie:
Obecnie dostępne są już pierwsze moduły kursu, a do września planujemy udostępnić kolejne, aby Twoje dziecko mogło płynnie rozpocząć naukę. Pozostałe moduły będą sukcesywnie dodawane w trakcie roku szkolnego.

Po wykupieniu dostępu do dowolnego modułu, uczeń zyskuje możliwość udziału w dyżurach nauczyciela – spotkaniach online, na których może zadawać pytania i wyjaśniać wszelkie wątpliwości. Dyżury odbywają się dwa razy w tygodniu: w ciągu dnia i wieczorem – do wyboru.

Wstępne terminy dyżurów w roku szkolny ’25/’26:

  • poniedziałki 13:30,
  • wtorki 18:10.

Twoje dziecko potrzebuje większego wsparcia niż tylko nagrane lekcje i dyżury nauczyciela?

Możecie skorzystać z rozszerzonej wersji Kursu, która obejmuje dostęp do regularnych, grupowych zajęć online z nauczycielem.

Zajęcia odbywają się raz w tygodniu, w godzinach porannych, według ustalonego programu dostosowanego do potrzeb dzieci w edukacji domowej.

To doskonałe uzupełnienie samodzielnej nauki – pomaga utrwalić materiał, uporządkować wiedzę i daje możliwość zadawania pytań na bieżąco.

Zajęcia prowadzone są od początku września do końca maja i rozpoczynają się po zebraniu się grupy.

Do grupy można dołączyć w dowolnym momencie.

Wstępny termin lekcji na żywo w roku szkolny ’25/’26:

  • wtorki 10:00 – 10:50

Twoje dziecko nie potrzebuje dostępu do nagrań i arkuszy zadań?

Możecie skorzystać z pakietu LIve, w którym uczeń ma dostęp do regularnych, grupowych zajęć online.

Spotkania te prowadzone są według ustalonego programu i stanowią doskonałe uzupełnienie samodzielnej nauki — pomagają utrwalić materiał, uporządkować wiedzę i dają możliwość zadawania pytań.

Do grupy można dołączyć w dowolnym momencie.

Dlaczego nagrałam lekcje?

Nauka matematyki wymaga stopniowego budowania zrozumienia i umiejętności.

Zdecydowałam się oferować kurs złożony nie z jednej, czy dwóch lekcji w tygodniu, jak to ma miejsce na tradycyjnych kursach, ale z tylu lekcji, ile jest w stanie w danym momencie zrealizować uczeń. Zależało mi na tym, żeby uczeń mógł realizować podstawę programową pomału, bez pośpiechu.  

Dzięki nagranym lekcjom, dziecko ma dostęp do mojej wiedzy i doświadczenia przez cały tydzień, a nie tylko podczas jednego, czy dwóch spotkań na żywo.

W razie jakichkolwiek trudności, każdy uczeń ma dostęp do spotkań na żywo z nauczycielem w czasie dyżurów, które odbywają się dwa razy w tygodniu. Zachęcam do przychodzenia na dyżury i wyjaśniania wszelkich wątpliwości na bieżąco!

A jeśli okaże się, że uczeń potrzebuje jeszcze więcej wsparcia, rytmu lub struktury, w każdej chwili może dołączyć do grupowych lekcji na żywo, które odbywają się raz w tygodniu i przebiegają według z góry ustalonego programu.

Zapisz dziecko na kurs już dziś!

Przewijanie do góry