Nie jest tajemnicą, że wielu uczniów ma trudności z rozwiązywaniem równań, ponieważ jest to dla nich proces abstrakcyjny, oparty na mechanicznych regułach. Wykorzystanie metody CPA (Concrete, Pictorial, Abstract) w nauczaniu rozwiązywania równań liniowych, pozwala nam na zbudowanie solidnego pomostu między tym, co uczniowie widzą i dotykają, a symbolicznym zapisem.

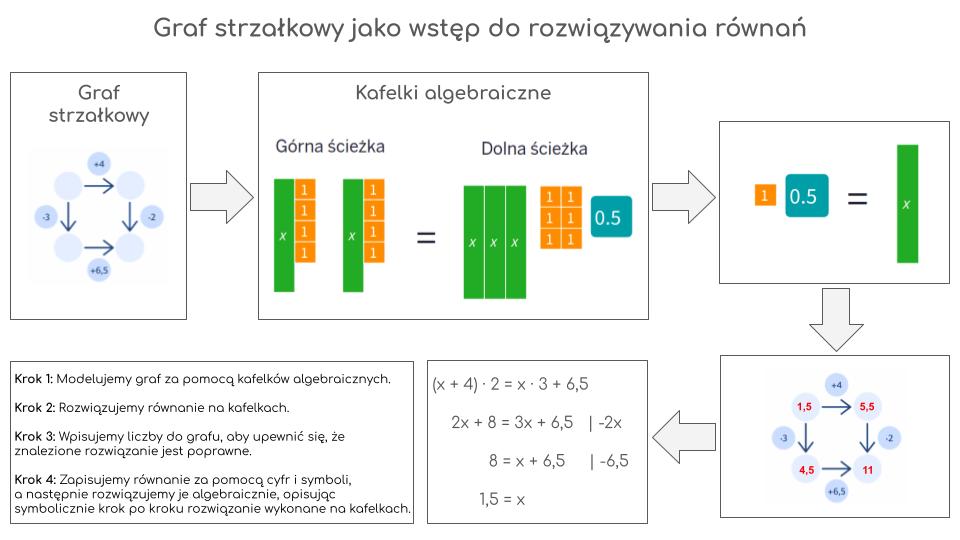
1. Graf strzałkowy (Pictorial/Schematyczny)
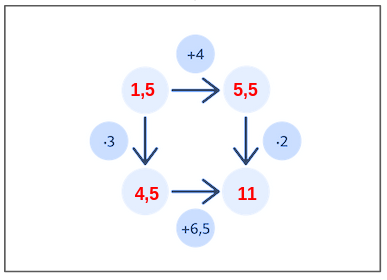
Graf strzałkowy wizualizuje proces myślowy stojący za równaniem. Uczeń widzi, co po kolei dzieje się z niewiadomą, zmuszając go do myślenia o kolejności działań.
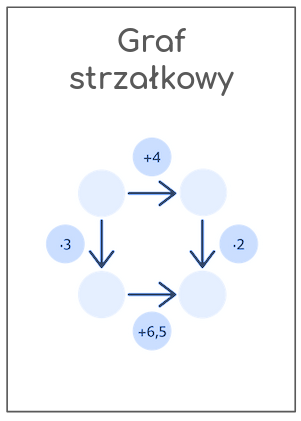
2. Kafelki algebraiczne (Concrete/Fizyczny)
Tłumaczenie grafu na kafelki algebraiczne jest kluczowym krokiem. Rozwiązanie staje się fizycznym działaniem polegającym na usuwaniu elementów i dzieleniu ich na równe grupy. Działania te nie są już tylko symbolami, ale konkretnymi operacjami wykonywanymi na materialnych pomocach.
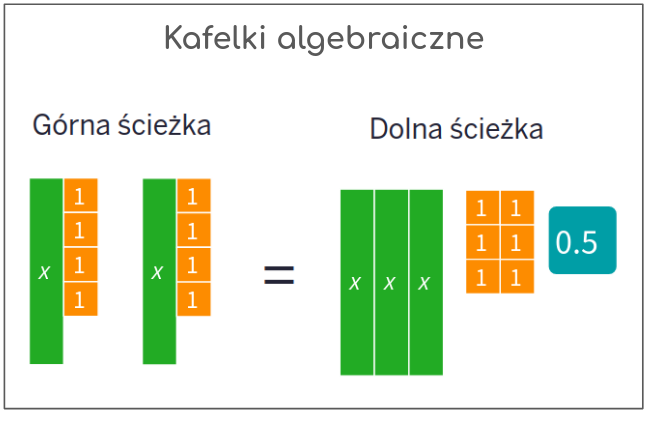
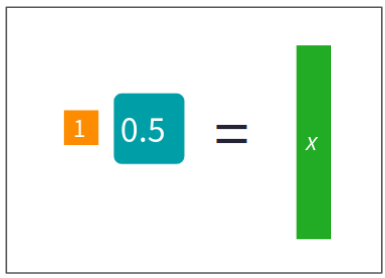
3. Łączenie kroków z algebrą (Abstract/Abstrakcyjny)
Dopiero po tym, jak uczeń kilkukrotnie wykona operacje na kafelkach (i zweryfikuje wynik, podstawiając go do grafu!), jest gotowy do zapisywania równań w sposób symboliczny.

Rozwiązując abstrakcyjne równanie, uczeń nie “przerzuca” niczego w oparciu o niezrozumiałe regułki, ale świadomie zapisuje kroki, które wcześniej wykonywał na kafelkach. Dzięki temu eliminujemy mechaniczne stosowanie reguł.
Warto zainwestować czas w pracę na konkretach. To fundament pod przyszłą naukę funkcji i bardziej złożonych zagadnień algebraicznych.