Witaj w bibliotece artykułów!
Matematyka może być fascynująca i przystępna dla każdego! W tej sekcji zebrałam wszystkie moje artykuły, które mają jeden cel: pokazać Ci, jak budować prawdziwe zrozumienie matematyki. Zapraszam do przeglądania poniższych kategorii. Znajdziesz tu wszystko, od innowacyjnych metod nauczania z wykorzystaniem Klocków Cuisenaire’a, przez porady dotyczące dyskalkulii, aż po sposoby na skuteczne rozwiązywanie problemów.
Baza artykułów jest stale rozwijana, więc zaglądaj tu regularnie po nowe inspiracje i wiedzę!
Spis treści
Klocki Cuisenaire’a
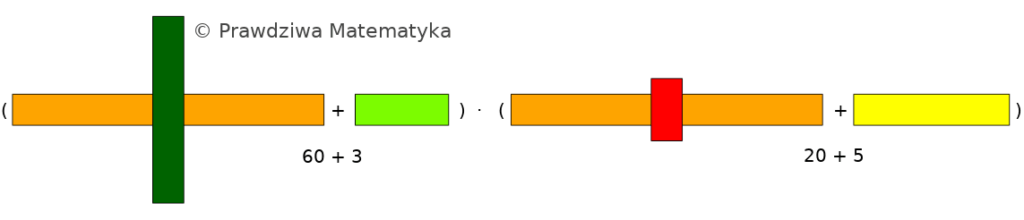
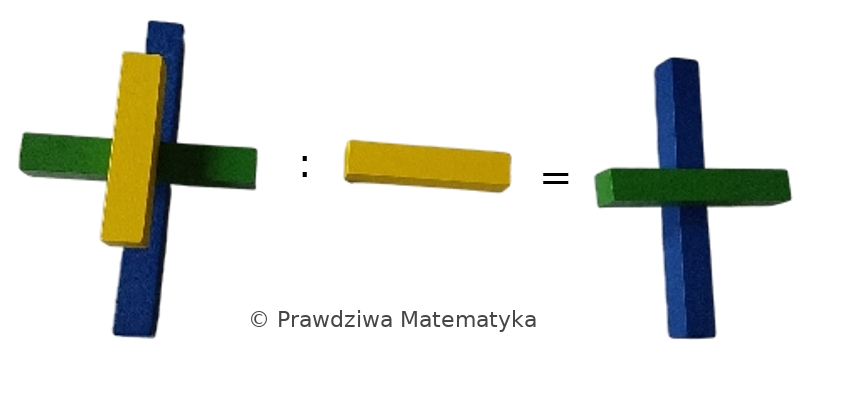
Klocki Cuisenaire’a – rozkład na czynniki pierwsze
W poprzednim artykule odkrywaliśmy liczby parzyste, nieparzyste, pierwsze i złożone za pomocą Klocków Cuisenaire’a. Dziś zanurzymy się głębiej w świat liczb, badając dzielniki oraz fascynujące pojęcie rozkładu na czynniki pierwsze…
Klocki Cuisenaire’a – liczby parzyste, nieparzyste, pierwsze i złożone
W świecie Klocków Cuisenaire’a abstrakcyjne pojęcia matematyczne, takie jak liczby parzyste, nieparzyste i pierwsze, nabierają konkretnego, wizualnego kształtu. Dzięki prostym operacjom na klockach, dzieci mogą samodzielnie odkryć i zdefiniować te…
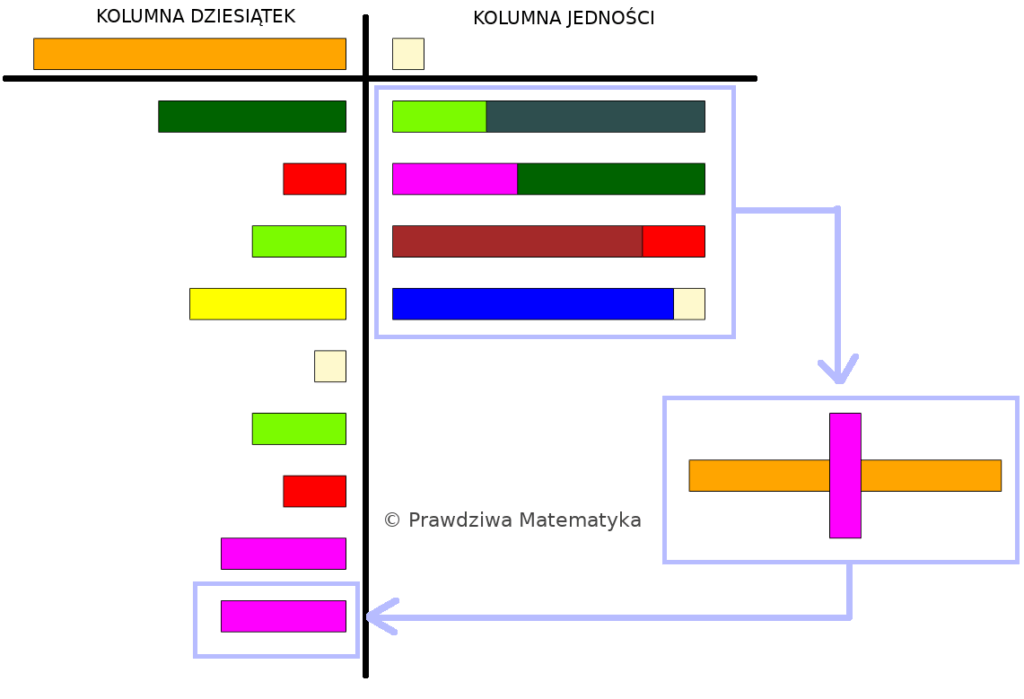
Klocki Cuisenaire’a – mnożenie liczb wielocyfrowych
W poprzednim artykule zgłębialiśmy podstawowe zasady mnożenia i jego kluczowe własności, takie jak przemienność, łączność i rozdzielność. Dziś kontynuujemy naszą podróż, skupiając się na praktycznym zastosowaniu prawa rozdzielności w mnożeniu…
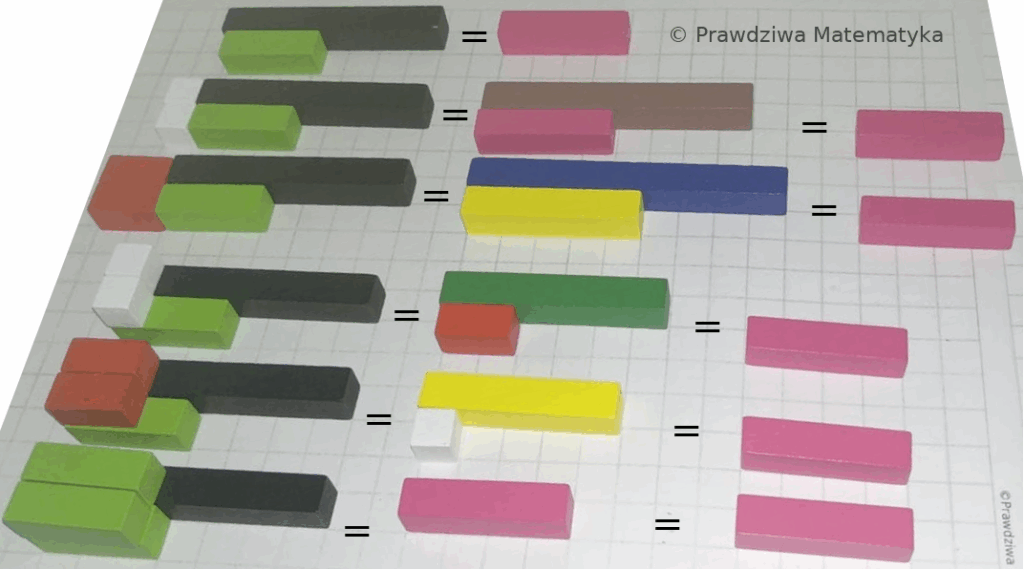
Klocki Cuisenaire’a – mnożenie liczb naturalnych
Kontynuujemy naszą podróż po świecie arytmetyki z Klockami Cuisenaire’a! Po opanowaniu dodawania i odejmowania, nadszedł czas na mnożenie – operację, która bywa dla wielu dzieci (i dorosłych!) bardziej abstrakcyjna. Klocki…
Klocki Cuisenaire’a – dodawanie i odejmowanie liczb naturalnych – przekraczanie progu i pożyczanie
W poprzednich artykułach odkrywaliśmy, jak Klocki Cuisenaire’a pomagają zrozumieć podstawowe operacje dodawania i odejmowania, a także fundamentalne własności tych działań. Dziś idziemy o krok dalej i zmierzymy się z arcyważnymi…
Klocki Cuisenaire’a – dodawanie i odejmowanie liczb naturalnych
Witajcie w kolejnym artykule z naszej serii o wykorzystywaniu Klocków Cuisenaire’a! Jeśli w poprzednich częściach zafascynowała Was ich moc w rozwijaniu wyobraźni przestrzennej, dziś ponownie zanurzymy się w ich równie…
Klocki Cuisenaire’a – konwencje
Czy matematyka bywa dla Twojego dziecka, a może i dla Ciebie, abstrakcyjnym labiryntem cyfr i symboli? Pamiętasz, jak trudno było zrozumieć, czym właściwie jest \(3 \cdot 5\) albo czym różni…
Klocki Cuisenaire’a a kształtowanie wyobraźni przestrzennej – BUDOWLE TRÓJWYMIAROWE
Dzień dobry, przyszli architekci i inżynierowie! Właśnie dotarliśmy do ostatniego, ekscytującego etapu naszej serii o rozwijaniu wyobraźni przestrzennej z Klockami Cuisenaire’a. Dziś zanurzymy się w świat trójwymiarowych konstrukcji i ich…
Klocki Cuisenaire’a a kształtowanie wyobraźni przestrzennej – ODBICIA & OBROTY
Po tym, jak opanowaliście sztukę obrotów i odbić, nadszedł czas, aby połączyć te umiejętności i zmierzyć się z naprawdę pasjonującymi wyzwaniami. Ten etap wymaga już solidnych podstaw, więc upewnijcie się,…
Klocki Cuisenaire’a a kształtowanie wyobraźni przestrzennej – ODBICIA
Czas na kolejny krok w rozwoju wyobraźni przestrzennej! Dziś skupimy się na odbiciach i koncepcji symetrii, wykorzystując nasze Klocki Cuisenaire’a. Czy zastanawiałeś się kiedyś, jak wyglądałby dany obiekt, gdybyś zobaczył…
Klocki Cuisenaire’a a kształtowanie wyobraźni przestrzennej: OBROTY
Witajcie w kolejnej części serii o klockach Cuisenaire’a i usprawnianiu prawej półkuli mózgu! Dziś skupiamy się na fascynującym świecie obrotów. Zrozumienie ruchu w geometrii to kluczowa umiejętność, która towarzyszy nam…
Klocki Cuisenaire’a a kształtowanie wyobraźni przestrzennej: ,,TANGRAM”
Badania neurologiczne rzucają światło na funkcjonowanie naszego mózgu, wskazując na odrębne funkcje obu półkul. Podczas gdy lewa półkula jest naszym centrum logiki, języka i sekwencyjnego myślenia, to prawa półkula odpowiada…
Klocki Cuisenaire’a a relacje między wielkościami
Gdy po raz pierwszy widzimy Klocki Cuisenaire’a, często myślimy: ,,Ale słodkie, to na pewno dla przedszkolaków!” 😀 I owszem, są one fantastyczne dla najmłodszych, pomagając im zrozumieć liczby i podstawy…
Pierwsze kroki z Klockami Cuisenaire’a
W świecie nauki matematyki, gdzie abstrakcja często bywa wyzwaniem, Klocki Cuisenaire’a jawią się jako oaza konkretu i intuicji. Ale zanim zagłębimy się w szczegółowe lekcje i zaawansowane zastosowania, warto poświęcić…
Klocki Cuisenaire’a – poznaj pomoc, która ułatwia naukę matematyki!
Zastanawiasz się, jak w prosty i angażujący sposób pomóc dziecku zrozumieć matematykę? Klocki Cuisenaire’a to świetne narzędzie, które od lat wspiera nauczycieli i rodziców w nauczaniu podstawowych pojęć matematycznych. Ale…
Matematyka od nowa
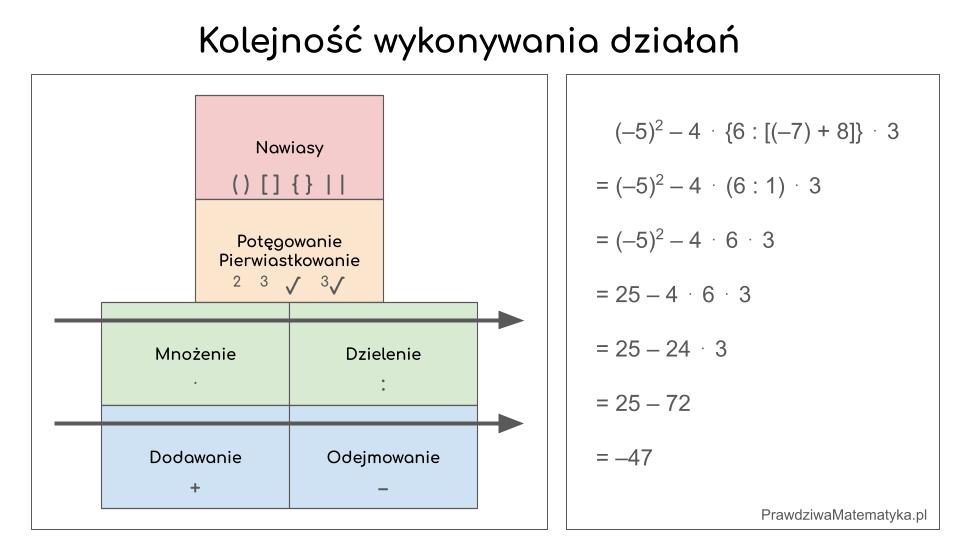
Kolejność wykonywania działań w oparciu o ich hierarchię
Obliczając wartości wyrażeń arytmetycznych kluczowe jest stosowanie się do ściśle określonej kolejności wykonywania działań. Zamiast traktować tę zasadę jako zbiór arbitralnych reguł, proponuję podejście oparte na logicznej hierarchii “mocy” operacji…
Radość z sukcesu w nauce: Jak odblokować wewnętrzną motywację dziecka
Doświadczenie jednoznacznie pokazuje: najskuteczniejsza motywacja wynika z głębokiego poczucia sukcesu. To autentyczna radość z rozwiązania zadania, które było odpowiednio wymagające, to satysfakcja z poczucia postępu. Ta wewnętrzna siła jest tarczą…
Doświadczenie osobiste w nauce: Dlaczego matematyka zaczyna się w piaskownicy?
Skuteczna edukacja polega na czymś więcej niż tylko na przekazywaniu gotowych formuł. Opiera się na doświadczeniu osobistym w nauce, które dziecko buduje od pierwszych chwil życia (w domu, w piaskownicy,…
Prawdziwa Motywacja: Jak rozbudzić w dziecku wewnętrzną potrzebę nauki?
Dlaczego motywacja jest kluczowa Motywacja jest siłą napędową każdego procesu uczenia się. To ona dostarcza energię i wyznacza kierunek działania, bezpośrednio wpływając na jego jakość. Dziecko, które posiada prawdziwą motywację,…
Szkoła jako laboratorium życia: Jak wspierać niezależne myślenie i dojrzałość społeczną dziecka
Współczesna szkoła to znacznie więcej niż tylko miejsce, gdzie przekazuje się suchą wiedzę. To kluczowe środowisko, w którym dzieci spędzają znaczącą część swojego życia, a tym samym kształtują się ich…
Schematy wiedzy w nauce matematyki
Jak działa mózg matematyka, czyli dlaczego solidne “fundamenty” są kluczowe w nauce Często mówimy o “fundamentach” i “budowaniu bazy” w nauce matematyki. W psychologii poznawczej te fundamenty mają konkretną nazwę:…
Matematyka a praktyka
Uczniowie, mimo znajomości wzorów i procedur, często mają trudności z ich zastosowaniem w praktycznych sytuacjach. W tym wpisie poruszę istotny aspekt nauczania matematyki, który często jest pomijany, a mianowicie umiejętność…
Matematyka a konwencje kulturowe
Jako nauczycielka matematyki z wieloletnim doświadczeniem, pragnę zwrócić Waszą uwagę na ważny aspekt edukacji matematycznej, który często jest pomijany. Choć logika jest fundamentem tej dziedziny, to bardzo istotne są konwencje,…
Matematyka a logika
Matematyka nie jest tylko przedmiotem, który wymaga opanowania zestawu procedur – jest to dziedzina, w której zrozumienie logicznych zasad jest fundamentem skutecznego uczenia się. Jako nauczycielka matematyki z wieloletnim doświadczeniem,…
Kiedy liczba jest podzielna przez 13? Regułka kontra zrozumienie
Wyobraź sobie, że jesteś w szkole na lekcji matematyki i uczysz się nowej regułki matematycznej, a konkretnie – jak sprawdzić, czy dana liczba jest podzielna przez 13. Oto procedura, którą…
Jak oceniać?
Kryteria oceny i ich zastosowanie w matematyce (cz.III)
Samoocena z wykorzystaniem kryteriów oceny – jak to wygląda w praktyce? Kiedy rozpoczynam współpracę z nową grupą, na samym początku omawiam z dziećmi kryteria oceny, które będę stosowała na zajęciach. Omawiam…
Kryteria oceny i ich zastosowanie w matematyce (część II)
Kryteria oceny specyficzne dla zadania Kryteria oceny specyficzne dla zadania to narzędzie, które umożliwia ocenianie postępów uczniów na podstawie konkretnych wskaźników odnoszących się do danego zadania. W przeciwieństwie do ogólnych…
Kryteria oceny i ich zastosowanie w matematyce (część I)
W procesie oceniania, kluczową rolę odgrywają odpowiednio zaprojektowane zadania, które dostarczają nauczycielom ogromnej ilości informacji. Jednak, aby te dane miały wartość, trzeba je właściwie ocenić. Kryterium oceny to narzędzie, które…
Aktywności matematyczne jako źródło informacji o uczniu
Jednym z moich celów, jako nauczycielki matematyki, jest zrozumienie, jak uczniowie myślą i jak łączą różne matematyczne pojęcia. Zamiast skupiać się na testach, które sprawdzają tylko końcowy wynik, staram się…
Wywiad diagnostyczny
Moim celem, jako nauczycielki matematyki, nie jest nauczenie uczniów rozwiązywania różnych typów zadań, ale przede wszystkim wsparcie ich w uzyskaniu głębokiego zrozumienia zasad, które rządzą matematyką. Uważam, że kluczem do…
Obserwacja jako klucz do zrozumienia ucznia
Każdy nauczyciel codziennie zdobywa cenne informacje o swoich uczniach. Ich wypowiedzi, strategie rozwiązywania problemów, sposób organizacji pracy – to wszystko daje wskazówki, jak myślą i na jakim etapie rozwoju matematycznego…
Ocena jako narzędzie w nauczaniu
Często, gdy myślimy o ocenianiu w szkole, przychodzą nam do głowy testy końcowe – sprawdziany, które podsumowują cały dział i pokazują, ile uczeń zapamiętał. To ocenianie sumatywne (podsumowujące), które ma…
Indywidualizacja nauczania
Przykłady różnicowania nauczania: praca w grupach
Elastyczne grupowanie – jak skutecznie wspierać naukę matematyki Praca w grupach to nie tylko metoda nauczania, ale przede wszystkim sposób na rozwijanie umiejętności współpracy i komunikacji. Uczniowie uczą się od…
Przykłady różnicowania nauczania: lekcje na różnych poziomach
Jednym z najskuteczniejszych sposobów różnicowania nauczania jest stosowanie lekcji na różnych poziomach. To podejście pozwala wszystkim uczniom osiągnąć te same cele edukacyjne, ale różni się ścieżkami, które prowadzą do ich…
Przykłady różnicowania nauczania: stacje zadaniowe
Stacje zadaniowe w nauczaniu matematyki Organizacja i zalety stacji zadaniowych Na początku mojej przygody z nauczaniem sądziłam, że uczniowie najlepiej uczą się poprzez tradycyjne metody, ale szybko przekonałam się, że…
Przykłady różnicowania nauczania: praca z całą klasą
Różnicowanie zadań w pracy z całą klasą Jednym z wyzwań w różnicowaniu nauczania jest tworzenie zadań, które będą skupiały się na kluczowym zagadnieniu matematycznym i jednocześnie uwzględniały różnorodne potrzeby uczniów…
Elementy nauczania: środowisko, treść, proces i produkt
Jednym z największych wyzwań w nauczaniu jest znalezienie sposobu na skuteczne dostosowanie nauczania do uczniów. Każde dziecko jest inne – ma inne doświadczenia, zainteresowania, poziom gotowości do nauki i sposoby…
Uczeń też człowiek…
Każde dziecko przynosi ze sobą własne doświadczenia, zainteresowania i sposoby uczenia się. Nauczyciel, który chce skutecznie różnicować nauczanie, powinien zacząć od głębokiego poznania swoich uczniów – nie tylko ich umiejętności…
Ustal jasne cele dla swoich uczniów
Każdy nauczyciel, który chce skutecznie różnicować nauczanie, musi zacząć od podstawowego pytania: „Co chcę, aby moi uczniowie wiedzieli, rozumieli i potrafili zrobić na końcu tej lekcji lub cyklu lekcji?” To…
Indywidualizacja nauczania – dlaczego warto?
Każde dziecko uczy się inaczej Od dawna nauczyciele akceptują fakt, że dzieci różnią się poziomem umiejętności czytania, pisania, a nawet sprawnością fizyczną. Jednak wciąż nie dla wszystkich jest oczywiste, że podobne…
Rozwiązywanie problemów
Podziel lekcję na 3 etapy
Matematyka nie polega na wkuwaniu wzorów i powtarzaniu procedur. Prawdziwe zrozumienie pojawia się, gdy dzieci same odkrywają zależności i szukają własnych strategii rozwiązania problemów. Właśnie dlatego tak ważne jest nauczanie…
Narzędzia matematyczne (część III)
Jako nauczycielka matematyki często obserwuję, jak dzieci uczą się nowych pojęć. Widzę, że nie każde dziecko od razu odnajduje się w abstrakcyjnym świecie liczb i symboli – wiele z nich…
Narzędzia matematyczne (część II)
Jako nauczycielka matematyki wierzę, że prawdziwe zrozumienie matematyki nie wynika z mechanicznego powtarzania procedur, lecz z głębokiego pojmowania zależności między liczbami, operacjami i strukturami. W tym kontekście często sięgamy po…
Narzędzia matematyczne (część I)
Jako nauczycielka matematyki zawsze poszukuję sposobów, by uczynić abstrakcyjne pojęcia bardziej dostępnymi dla moich uczniów. Jednym z najskuteczniejszych podejść jest wykorzystanie różnorodnych reprezentacji matematycznych. Czym są reprezentacje matematyczne? Reprezentację matematyczną…
Prowadzenie dyskusji w klasie (część II)
Ile podpowiadać, a ile pozostawić do odkrycia? Jako nauczyciele matematyki często stajemy przed trudnym dylematem: ile informacji przekazać uczniom, a ile pozwolić im odkryć samodzielnie? To jedno z największych wyzwań…
Prowadzenie dyskusji w klasie (część I)
Jako nauczycielka matematyki od lat obserwuję, jak istotną rolę odgrywają klasowe dyskusje w procesie edukacyjnym. Nie ma lepszego sposobu na pogłębienie zrozumienia matematycznych pojęć niż umożliwienie uczniom swobodnej wymiany myśli…
Wybór wartościowych zadań matematycznych cz. III
Jako nauczycielka matematyki, która stawia zrozumienie ponad pamięciowym opanowaniem materiału, jestem przekonana, że nie tylko wybór zadania, ale także przygotowanie się do jego wykorzystania w klasie ma ogromne znaczenie. Oto…
Wybór wartościowych zadań matematycznych cz. II
W mojej praktyce nauczycielskiej wielokrotnie przekonałam się, że właściwy dobór zadań matematycznych jest kluczem do efektywnego nauczania. Dziś chciałabym podzielić się refleksjami na temat projektowania zadań o wielu punktach wejścia…
Wybór wartościowych zadań matematycznych cz. I
Aby zadanie mogło pełnić funkcję problemu matematycznego, musi angażować uczniów na poziomie ich obecnego rozumienia oraz stanowić dla nich wyzwanie. Wybierając odpowiednie zadanie, warto wziąć pod uwagę trzy kluczowe aspekty:…
Przykłady wartościowych zadań
Zadania problemowe mogą być wykorzystywane zarówno do rozwijania zrozumienia pojęć matematycznych, jak i do nauki procedur. Ponadto, pomagają budować związki między pojęciami a procedurami, co sprzyja głębszemu zrozumieniu matematyki. Samo…
Wartościowe zadanie, czyli jakie?
Nauczanie matematyki poprzez rozwiązywanie problemów oznacza, że uczniowie poznają nowe treści matematyczne poprzez pracę nad zadaniami wymagającymi samodzielnego myślenia. Czym jest problem? Problemem nazywamy każde zadanie, dla którego uczniowie nie…
Nauczanie matematyki poprzez rozwiązywanie problemów
Tradycyjne nauczanie matematyki opiera się na podejściu, w którym nauczyciel prezentuje nowe pojęcie, uczniowie ćwiczą konkretną umiejętności, a dopiero na końcu rozwiązują zadania tekstowe, w których muszą wykorzystać zdobytą wiedzę…
Zrozumienie
Walka intelektualna
Jednym z najtrudniejszych aspektów nauczania matematyki jest pozwalanie uczniom na walkę intelektualną. Naszym instynktem jako nauczycieli jest, aby wkroczyć, podać rozwiązania i złagodzić frustrację. Ale jeśli celem jest zrozumienie relacyjne…
Atmosfera sprzyjająca nauce przez zrozumienie
Wyobraź sobie lekcję matematyki, w czasie której uczniowie z zaangażowaniem omawiają strategie, debatują nad rozwiązaniami i traktują błędy jako okazje do nauki. Tego rodzaju środowisko nie powstaje przypadkowo – wymaga…
Trzy metody nauczania
Kiedy myślimy o nauczaniu matematyki, często wyobrażamy sobie nauczyciela stojącego pod tablicą i wyjaśniającego krok po kroku procedury. Choć bez wątpienia metoda wykładowa ma swoje zalety, jest to tylko jedna…
Co powinno być w centrum – uczeń, czy procedura?
Dwa ostatnie wpisy poświęciłam opisom dwóch różnych podejść do nauczania – w pierwszym z nich stawiamy w centrum ucznia, a w drugim procedurę. Jeśli nie przeczytałaś jeszcze tych wpisów, zachęcam do…
Procedura w centrum uwagi
We wczorajszym wpisie opisałam przykład lekcji, która skoncentrowana była na uczniu. Dzisiaj przedstawię Wam przeciwieństwo tego podejścia, czyli lekcję skoncentrowaną na instrumentalnym zrozumieniu. Tego typu lekcja koncentruje się na nauczeniu…
Uczeń w centrum uwagi
Nauczanie matematyki nie musi być nudnym procesem polegającym na mechanicznym powtarzaniu schematów i reguł. Przykład klasy drugiej pokazuje, jak podejście zorientowane na ucznia – pozwalające dzieciom samodzielnie odkrywać i tworzyć…
Jak dzieci uczą się najlepiej? Konstruktywizm i teoria społeczno-kulturowa w praktyce edukacyjnej
Rozumienie, w jaki sposób dzieci uczą się, pozwala nauczycielom tworzyć bardziej efektywne i angażujące strategie nauczania. Dwie kluczowe teorie – konstruktywizm i teoria społeczno-kulturowa – rzucają światło na procesy uczenia…
Osiem fundamentów nauczania matematyki
Współczesne podejście do edukacji matematycznej wskazuje na znaczenie rozwijania nie tylko umiejętności proceduralnych, ale także głębokiego rozumienia koncepcji matematycznych. W pracy z dziećmi warto kłaść nacisk na osiem kluczowych Standardów Praktyki…
Pięć filarów matematycznej biegłości – jak budować prawdziwe zrozumienie matematyki?
Matematyka to znacznie więcej niż szybkie liczenie czy rozwiązywanie równań. Aby dziecko mogło naprawdę ją zrozumieć, potrzebuje wsparcia w rozwijaniu pięciu ściśle powiązanych ze sobą elementów matematycznej biegłości: Te pięć…
Dlaczego nauka matematyki musi opierać się na zrozumieniu, a nie tylko na regułkach?
Przez wiele lat nauczanie matematyki opierało się głównie na rozwijaniu proceduralnej sprawności – zdolności do szybkiego i poprawnego wykonywania działań matematycznych. Chociaż jest to ważna umiejętność, współczesne podejście do edukacji…
Dyskalkulia
Poznajcie Ronalda Davisa
Jednym z zaburzeń, które bardzo często towarzyszą dyskalkulii jest dysleksja, która kojarzy się głównie z trudnościami w nauce czytania, pisania i ortografii, jednak wiele osób z tym zaburzeniem ma unikalne…
Poznajcie Michała
W dzisiejszym odcinku serii “Poznajcie…” przedstawię Wam Michała, który prowadzi swoją własną firmę projektową w Wielkiej Brytanii. Historia Michała jest o tyle interesująca, że od najmłodszych lat mierzy się z dyspraksją oraz dysleksją. Dziś…
Drodzy Uczniowie z dyskalkulią
Jako nauczycielka matematyki wiem, że praca z liczbami może być wyzwaniem – szczególnie dla Was, którzy zmagacie się z dyskalkulią. Chciałabym Wam powiedzieć coś bardzo ważnego: Wasza dyskalkulia nie definiuje…
Przezwyciężyć dyskalkulię: nadzieja i wytrwałość to klucze do sukcesu
Życie z dyskalkulią może być wyzwaniem, ale nie musi definiować ludzkiego potencjału. Wiele wspaniałych postaci z przeszłości i teraźniejszości zmagało się z podobnymi trudnościami, przekształcając swoje wyzwania w siłę. Ich…
Pomoc dorosłym dyskalkulikom
Jako nauczycielka matematyki, każdego dnia spotykam się z uczniami, którzy mają różne trudności w nauce tego przedmiotu. Jednak dla osób z dyskalkulią, czyli zaburzeniem w przetwarzaniu informacji matematycznych, matematyka staje…
Matematyka w życiu nastolatków: Jak angażować starsze dzieci w codzienne wyzwania matematyczne
Wspieranie na co dzień dzieci, które mają trudności z matematyką wynikające z dyskalkulii (lub o innym podłożu), może być wyzwaniem, ale warto podjąć ten wysiłek, bo jest to świetna okazja, by…
Poznajcie Karolinę
Pozwólcie, że przedstawię Wam Karolinę, właścicielkę studia graficznego. Choć od najmłodszych lat borykała się z dyskalkulią, udało jej się odnieść sukces w pracy zawodowej. Oprócz dyskalkulii, Karolina ma jeszcze jedną przypadłość – synestezję. Przeczytajcie poniżej, co o…
Matematyka na co dzień: Jak rozwijać umiejętności matematyczne u dzieci w prostych czynnościach
Niezależnie od tego, czy Twoje dziecko wykazuje trudności w nauce matematyki charakterystyczne dla dyskalkulii, czy nie, wiele codziennych czynności może stać się okazją do bezstresowych ćwiczeń matematycznych. Okazuje się, że…
Jak pomagać dzieciom z dyskalkulią?
Dyskalkulia to trudność w nauce matematyki, która może prowadzić do frustracji, niskiej samooceny i wyzwań w codziennym życiu. Jednak odpowiednie podejście do nauki może pomóc takim dzieciom rozwijać się i…
Zaburzenia współistniejące z dyskalkulią – dysleksja
Dysleksja, podobnie jak inne zaburzenia edukacyjne, jest szeroko badana, a na jej temat jest dostępne znacznie więcej literatury naukowej niż na temat dyskalkulii. Szacuje się, że istnieje co najmniej dziesięć…
Zaburzenia współistniejące z dyskalkulią – dyspraksja
Dyskalkulia, czyli trudności w przyswajaniu matematyki, jest zaburzeniem, które rzadko występuje w izolacji. W rzeczywistości, około 40% osób z dyskalkulią zmaga się z dodatkowymi trudnościami, takimi jak zaburzenia uwagi (ADD)…
Osoby z dyskalkulią też mają swoje mocne strony
Dyskalkulia to wyzwanie, które może przytłaczać zarówno osoby nią dotknięte, jak i ich bliskich czy nauczycieli. Mimo, że symptomy mogą budzić niepokój, kluczowe jest zrozumienie, że nie każdy z objawów…
Czy ja mogę mieć dyskalkulię?
Dyskalkulia, choć często kojarzona z dziećmi, dotyka także dorosłych, którzy zmagają się z trudnościami związanymi z liczbami i pojęciami matematycznymi. W codziennym życiu może to prowadzić do licznych wyzwań, które…
Poznajcie Maję
Chciałabym przedstawić Wam dzisiaj Maję, która od najmłodszych lat boryka się z dyskalkulią. Maja, mimo wielu trudności, poradziła sobie w życiu i pracuje teraz w branży twórczej. Dyskalkulia, to nie…
Lęk przed matematyką – kiedy liczby stają się koszmarem
Matematyka to przedmiot, który wielu uczniom sprawia trudności. Ale dla niektórych dzieci – szczególnie tych z dyskalkulią – może stać się źródłem prawdziwego lęku. Co więcej, taki lęk może prowadzić…
Trudności z czasem i przestrzenią – zrozumieć dyskalkulię
Czy Twoje dziecko ma problem z punktualnością, orientacją w terenie lub zrozumieniem pojęcia czasu? A może zdarza mu się gubić w znanym miejscu lub mylić kierunki? Te trudności mogą być…
Czy moje dziecko może mieć dyskalkulię?
Dyskalkulia jest jednym z zaburzeń uczenia się, które dotyczy trudności w rozumieniu i przetwarzaniu liczb oraz pojęć matematycznych. Choć problemy z matematyką mogą być normalną częścią procesu edukacji, uporczywe trudności…
Jak żyć z dyskalkulią?
Dyskalkulia nie oznacza ograniczeń! Wiele osób z dyskalkulią osiągnęło spektakularne sukcesy. Przykłady takich osób to Cher czy Henry Winkler, którzy pokazali, że można realizować swoje marzenia pomimo trudności z liczbami…
Jak wspierać dziecko z dyskalkulią w domu?
Rodzice mogą odegrać ważną rolę w pomaganiu dziecku z dyskalkulią. Oto kilka prostych strategii, które możesz wprowadzić w życie w domu: 1. Gry rodzinne z liczbami Gry z kośćmi, domino…
Jak pomóc dziecku z dyskalkulią w szkole?
Dyskalkulia może być wyzwaniem, ale istnieje wiele strategii, które mogą pomóc dzieciom lepiej radzić sobie z matematyką w środowisku szkolnym. Oto 5 wskazówek: 1. Wykorzystywanie pomocy wizualnych i materiałów konkretnych…
Dyskalkulia: Historia Natalii i 3 kroki do oswojenia liczb
Praca z osobami z trudnościami w nauce matematyki to moja codzienność i z doświadczenia wiem, że nie wszystkie trudności w nauce to dyskalkulia! Z dyskalkulii się nie wyrasta, ale można…
Jak wspierać uczniów z dyskalkulią?
Dzieci z dyskalkulią mogą osiągać sukcesy w nauce matematyki, jeśli otrzymają odpowiednie wsparcie. Jednym z kluczowych elementów jest indywidualizacja nauczania. Dostosowanie tempa pracy do możliwości ucznia pozwala mu lepiej zrozumieć…
Dyskalkulia a codzienne trudności w nauce matematyki
Osoby z dyskalkulią często odczuwają frustrację i zniechęcenie w trakcie nauki matematyki. Nawet jeśli starają się jak najlepiej zrozumieć materiał, ich trudności wynikają z głębszych problemów neurologicznych, a nie z…
Przyczyny dyskalkulii – co kryje się za trudnościami?
Chociaż dyskalkulia wciąż nie jest w pełni zrozumiana, badania naukowe wskazują na kilka głównych przyczyn tego zaburzenia. Na pierwszym miejscu wymienia się nieprawidłowości neurologiczne, które prowadzą do różnic w strukturze…
Dyskalkulia – czym jest i jakie są jej objawy?
Dyskalkulia to zaburzenie, które coraz częściej pojawia się w dyskusjach na temat trudności w nauce. Choć mniej znana niż dysleksja, jest równie istotnym problemem, który może znacząco wpływać na codzienne…
Różności
2 lipca 2025 to szczególna data!
Dziś, 2. lipca, jesteśmy dokładnie w połowie roku. Ale DZIŚ dzieje się coś jeszcze, coś, co może zaskoczyć miłośników liczb i refleksji nad czasem! Od tej chwili jesteśmy bliżej roku…
Matematyka zaczyna się wcześniej, niż myślisz!
Zastanawiasz się, czy Twoje dziecko przejawia oznaki rozwoju umiejętności matematycznych, ale nie wiesz, jak je rozpoznać? A może odnosisz wrażenie, że Twoje dziecko rozwija się nieharmonijnie i martwisz się, że mimo…
Jak rozmawiać z małymi dziećmi o liczbach ujemnych?
Liczby ujemne mogą wydawać się trudne do zrozumienia na pierwszy rzut oka, ale w praktyce to pojęcie, które dzieci spotykają w życiu codziennym już od najmłodszych lat. Wystarczy spojrzeć na…
Co to są liczby pierwsze i dlaczego są tak ważne?
Liczby pierwsze są podstawą matematyki, a jednak często nie poświęca się im wystarczająco dużo uwagi. To liczby większe od 1, które dzielą się tylko przez 1 i przez siebie samą…
Zagadka, która zadziwi dziecko
Wykonaj poniższe kroki:1) Pomyśl dowolną liczbę.2) Pomnóż ją przez 2.3) Do wyniku dodaj 10.4) Podziel otrzymaną liczbę przez 2.5) Od wyniku odejmij pomyślaną na początku liczbę.Jaka liczba Ci wyszła? Spróbuj jeszcze raz!…
Matematyka w naturze: sekret ciągu Fibonacciego
Na pewno zauważyliście, że matematyka kryje się w otaczającej nas przyrodzie. Ciąg Fibonacciego, czyli seria liczb, w której każda następna jest sumą dwóch poprzednich (1, 1, 2, 3, 5, 8,…
Notatnik matematyczny – proste i bardzo efektywne narzędzie do nauki
Jeżeli nie prowadzisz jeszcze notatnika matematycznego, to bardzo Cię do tego zachęcam. Taki notatnik, to kluczowy krok w utrwalaniu wiedzy. Za każdym razem, kiedy uczysz się nowego zagadnienia, postaraj się…
Szkolny rozkład materiału
Jeżeli miałeś kiedyś w ręku szkolny rozkład materiału z matematyki, to być może zauważyłeś, że na każdy temat autorzy podręcznika przeznaczają zwykle jedną, czasem dwie, a jeszcze rzadziej trzy lekcje…
Z matematyką jest jak ze sztuką
Z matematyką jest jak ze sztuką – w sztuce każdy artysta postrzega to samo w nieco inny sposób. Każdy artysta ma swój unikalny sposób wyrazu. Analogicznie jest w matematyce –…
Prawdziwa Matematyka to sztuka
Uprawianie matematyki, jak każdej innej sztuki, wymaga zręczności i specjalnych umiejętności. Wiele osób postrzega matematykę jako skomplikowany zestaw oderwanych faktów, regułek oraz twierdzeń, które muszą być opanowane na pamięć i…
Prawdziwa Matematyka to język
Język matematyki jest bardzo precyzyjny. Opanowanie go pozwala nam porozumiewać się w sposób jasny i zrozumiały z innymi ludźmi na tematy związane z nauką, codziennymi sytuacjami oraz czystą matematyką. Jak…
Prawdziwa Matematyka to narzędzie
Nie tylko matematycy posługują się matematyką. Matematyka jest narzędziem, które każdy z nas wykorzystuje na co dzień do rozwiązywania zarówno abstrakcyjnych, jak i praktycznych problemów. W świecie, w którym żyjemy,…
Prawdziwa Matematyka to nauka o schematach i relacjach
Matematyczny sposób myślenia towarzyszy nam w codziennym życiu nawet wtedy, kiedy sobie tego nie uświadamiamy. Z jednej strony, matematyka uczy nas uniwersalnych sposobów porządkowania, analizowania i syntezowania informacji. Te pożyteczne…
Prawdziwa Matematyka to sposób myślenia
W matematyce powtarzają się pomysły oraz relacje między nimi. Stanowią one nić, która spaja pozornie niezwiązane ze sobą zagadnienia. Relacje mogą być bardzo bliskie, jak podobieństwo między równoważnymi zapisami tego…
Prawdziwa Matematyka to…
Bardzo często ludzie utożsamiają matematykę z arytmetyką albo postrzegają ją nieco szerzej, jako zbiór nie powiązanych ze sobą działów, np. algebra i geometria. Ja patrzę na matematykę zupełnie inaczej. Dla…
O kim powiesz, że ktoś jest dobry z matematyki?
Na podstawie jakich przesłanek wysuwasz o kimś taki wniosek? Czy Ty jesteś dobry/a z matematyki? Co dokładnie sprawia, że tak o sobie myślisz? Co jest według Ciebie ważne w matematyzowaniu?…
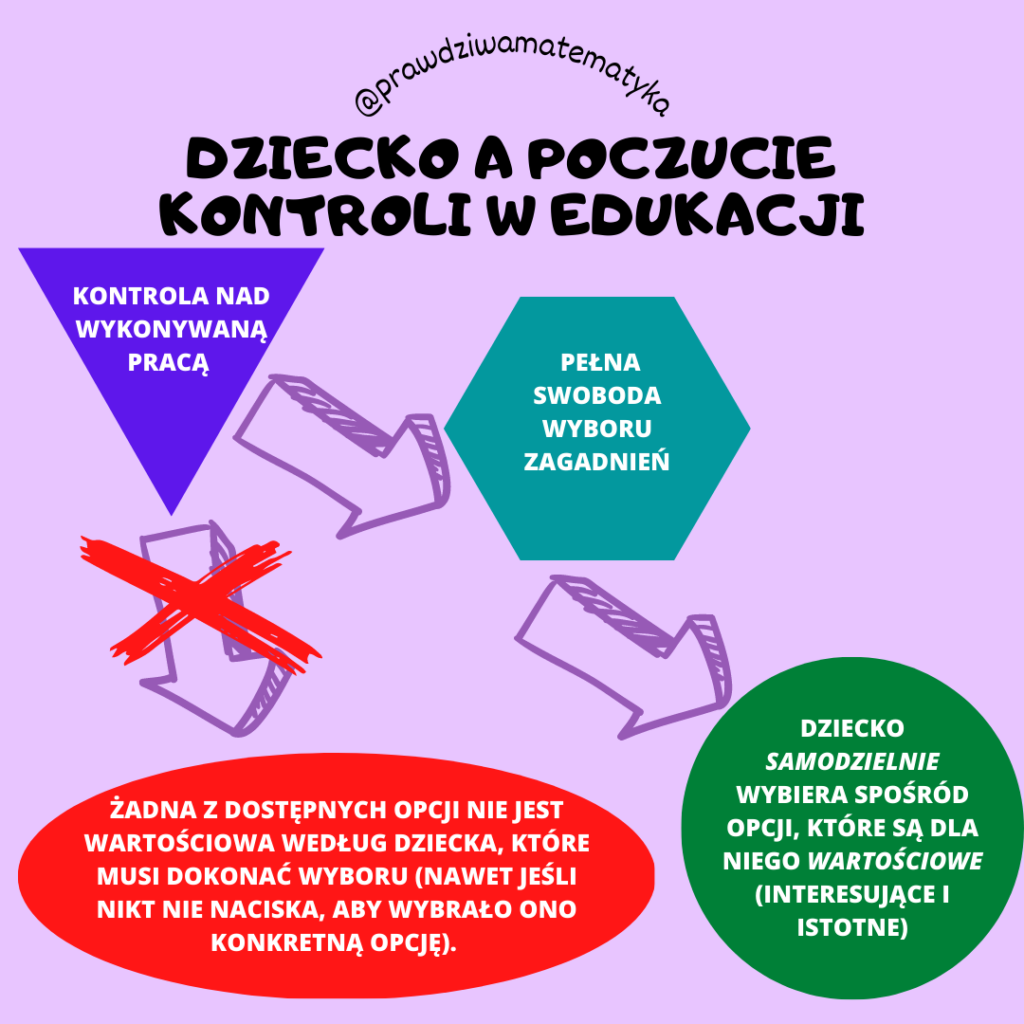
Dziecko a poczucie kontroli w edukacji
Aby dziecko prawdziwie chciało się uczyć, musi mieć poczucie kontroli nad wykonywaną pracą. Ta kontrola, to świadomość swobody w wybieraniu zagadnień, które są dla niego interesujące i istotne. Swoboda wyboru…
Klucze do sukcesu w nauce!
Badania naukowe pokazały, że duży wpływ na osiągnięcie sukcesu w nauce mają: KONTROLA Kontrola, o której mowa, to swoboda w doborze tematów oraz form pracy, a także możliwość dowolnej zmiany…
Skupienie
Nieukończone zadania zajmują naszą krótkoterminową pamięć, a przez to rozpraszają nas i nie pozwalają skupić się w pełni na najważniejszych pracach. Żeby uwolnić umysł od pamiętania o tym, co mamy…
Zrozumienie kluczem do zapamiętania
Kluczem do trwałego zapamiętywania jest zrozumienie materiału, który mamy opanować. O wiele bardziej opłaca się nam wkładać wysiłek w rozumienie zagadnień, a nie ich bezmyślne zapamiętywanie (wkuwanie). Kiedy próbujemy zrozumieć…
Dlaczego konstruktywizm?
Co to jest KONSTRUKTYWIZM? Na początku XX wieku John Dewey udowodnił doświadczalnie, że PROCES UCZENIA SIĘ przebiega najpełniej wtedy, gdy UCZEŃ JEST AKTYWNIE ZAANGAŻOWANY W NAUKĘ oraz ma okazję do…
Od czego zależy poziom trudności zadania?
Czynniki wpływające na ocenę poziomu trudności zadania przez dzieci Która wartość jest nieznana?W zadaniach dotyczących dodawania i odejmowania najłatwiejsze są zadania: Pozostałe typy zadań zwykle sprawiają dzieciom większe trudności. Czy…
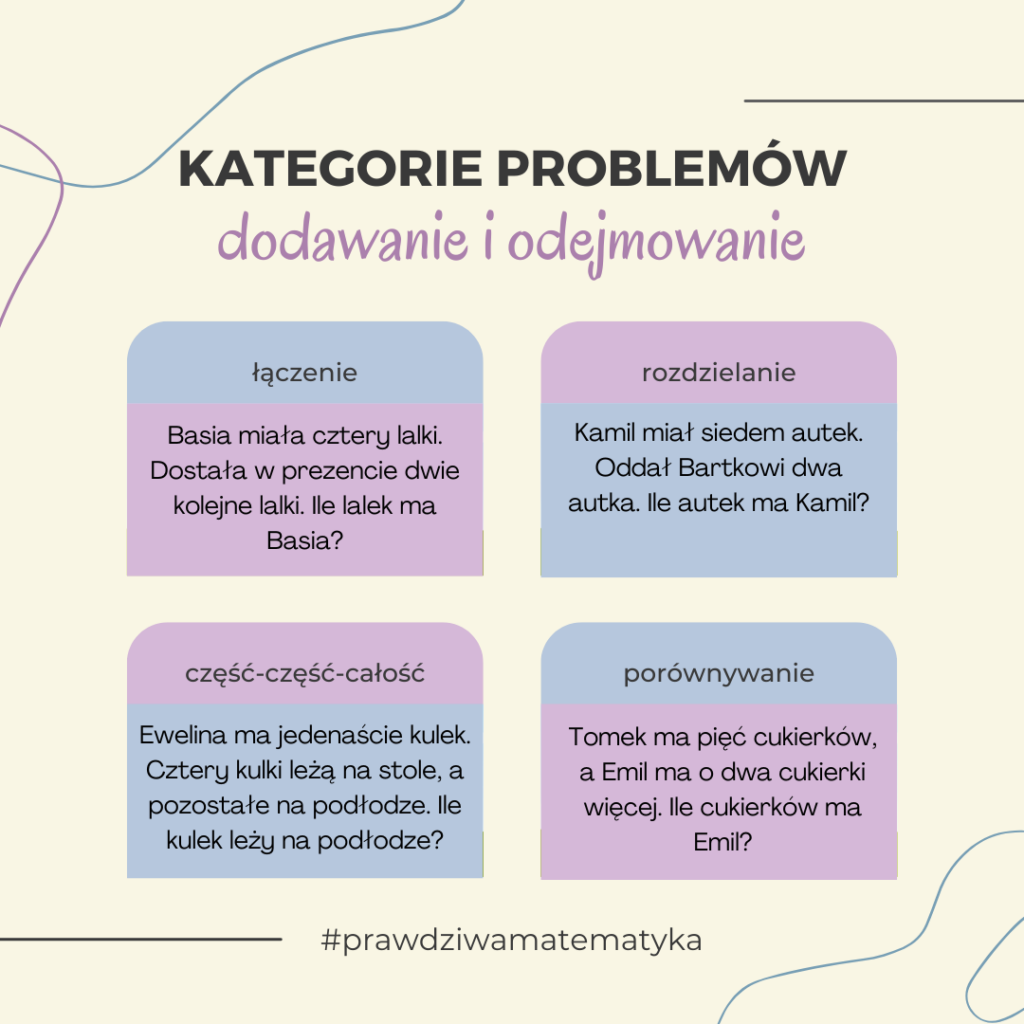
Kategorie problemów – dodawanie i odejmowanie
Zadania dotyczące dodawania i odejmowania klasyfikuje się w cztery szerokie grupy na podstawie akcji lub relacji, która pojawia się w problemie: W tych czterech grupach wyróżnia się łącznie JEDENAŚCIE typów…
Dlaczego uczymy się matematyki?
Odpowiedzi dzieci A co myśli Twoje dziecko? Dlaczego uczymy się matematyki?
Twoje dziecko nie musi wykuwać tabliczki mnożenia na pamięć
Podstawa programowa nie narzuca dzieciom obowiązku znajomości tabliczki mnożenia na pamięć. Wręcz przeciwnie – wymaga ona, aby DZIECI STOSOWAŁY WŁASNE STRATEGIE PRZY WYKONYWANIU OBLICZEŃ! Jak to rozumieć? Zamiast kazać dzieciom…
Jak uczyć mnożenia?
Eksperyment W 2001 r. Park i Nunes przeprowadzili eksperyment, którego celem było sprawdzenie, w jaki sposób rozwija się u dzieci pojęcie mnożenia. Dzieci zostały podzielone na dwie grupy – w…
Relacja partnerska w nauczaniu matematyki
Relacja partnerska to relacja, w której traktujemy drugiego człowieka jak pełnowartościową istotę ludzką. Chcemy w pełni uczestniczyć w jego rozwoju – szczerze interesują nas jego pomysły, wiedza, umiejętności. Relacja partnerska…
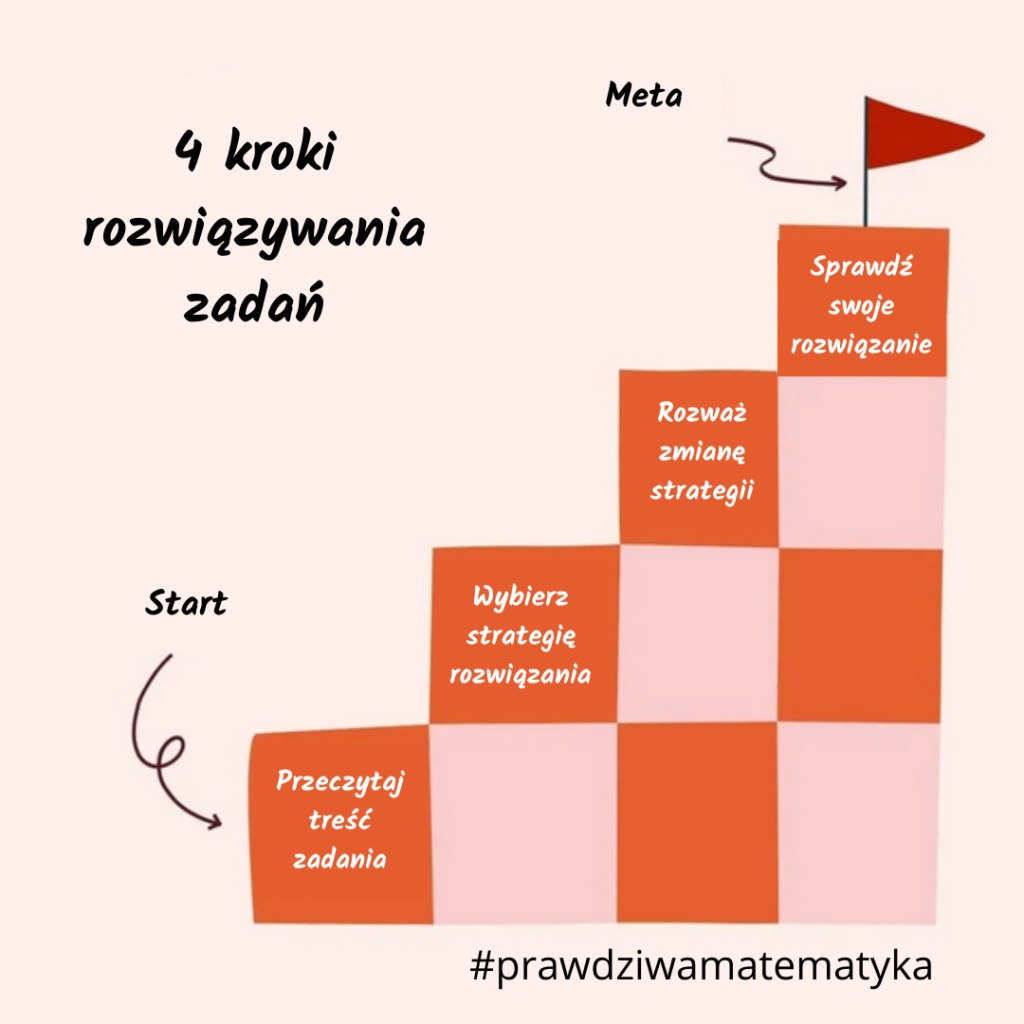
4 kroki rozwiązywania zadań
KROK 1. – przeczytaj treść zadania Treść zadania trzeba przeczytać uważnie i ze zrozumieniem. Jeżeli coś jest niezrozumiałe, warto przeczytać treść jeszcze raz. W zrozumieniu polecenia może pomóc powtórzenie treści…
Motywacja zewnętrzna, czy motywacja wewnętrzna?
Język chęci a język motywacji Pytając „co ją zmotywowało do wyruszenia na biegun?”, mamy na myśli odpowiedź na pytanie „dlaczego wyruszyła na biegun?”. Możliwe odpowiedzi wyrażone w „języku chęci”: Można…
Autorytet oparty na władzy, czy wiedzy?
Autorytet oparty na władzy Autorytet oparty na władzy ucieleśnia relację siły, w której posłuszeństwo wymuszane jest karą lub groźbą kary, nagrodą lub nadzieją na nagrodę. Autorytet oparty na wiedzy Autorytet…
Rozumie, czy nie rozumie?
Co to znaczy „rozumieć”? Rozumieć, to znaczy wiedzieć CO robić, JAK to robić i DLACZEGO akurat tak. Czy uczeń z ilustracji „rozumiał” jak oblicza się pole prostokąta? Nie. Wydawało mu…
Rozumowanie multiplikatywne
Dziecko jest w stanie samo skonstruować relację mnożenia! Nauczanie, które pomaga dzieciom budować struktury wiedzy, a nie koliduje z ich kreatywnością, dostarcza uczniom zasobów do wykorzystania przy mierzeniu się nowymi…
Formalny zapis dodawania
„… Mimo ich najlepszych intencji, presja, którą niektórzy rodzice wywierają na nauczycieli, aby zmuszali dzieci do zapisywania matematyki w sposób formalny, jest niekorzystna, szczególnie dotyczy to formalnego zapisywania dodawania, które…
Czy myślenie proporcjonalne jest trudne?
Nauczyciele narzekają, że uczniowie nie radzą sobie z ułamkami, ale zapominają, że trudności dzieci wynikają z tego, że nie pozwala się im na rozwinięcie jakiejkolwiek intuicji dotyczącej myślenia proporcjonalego. Najpierw…
Mnożenie przez 10 to dodawanie zera. Naprawdę???
PROBLEM Kiedy dzieci uczą się: Ani pierwsze, ani drugie nie ma niczego wspólnego z matematyką! Nie pomaga to zrozumieć, o co chodzi w mnożeniu, ani jak działa system pozycyjny. ROZWIĄZANIE…
Matematyka szkolna a Prawdziwa Matematyka
Matematyka szkolna, to matematyka, którą dzieci robią bez zrozumienia, naśladując algorytmy i metody podane przez nauczyciela. Prawdziwa matematyka, to matematyka, którą dzieci przeżywają, eksplorują, rozumieją i tworzą. Czy wolisz żeby…
Matematyzowanie czy “historia matematyki”?
Na pewno zgodzisz się ze mną, że uczenie się polega na budowaniu zrozumienia. Ucząc dziecko polskiego, pomagamy mu stać się pisarzem poprzez angażowanie go w proces pisania. Ucząc dziecko biologii,…
Czym się różni NAUCZYCIEL MATEMATYKI od PRAWDZIWEGO MATEMATYKA?
NAUCZYCIEL MATEMATYKI W „matematyce szkolnej”, nauczyciel postrzegany jest jako fontanna tryskająca wiedzą. Nauczyciel rozumie, że matematyka obejmuje przeróżne fakty, umiejętności, wzory oraz algorytmy. Nauczyciel wierzy, że matematyka może być przekazana,…
Co to znaczy MATEMATYZOWAĆ?
MATEMATYZOWAĆ – modelować, tworzyć schematy, strukturyzować otaczający nas świat w sposób matematyczny.
Nauczać, a uczyć się
Zauważ, jak blisko spokrewnione są ze sobą wyrazy “nauczanie” i “uczenie się”. Niech oba procesy będą równie blisko siebie w czasie naszych zajęć z dziećmi. Starajmy się, aby nauczanie przeplatało…