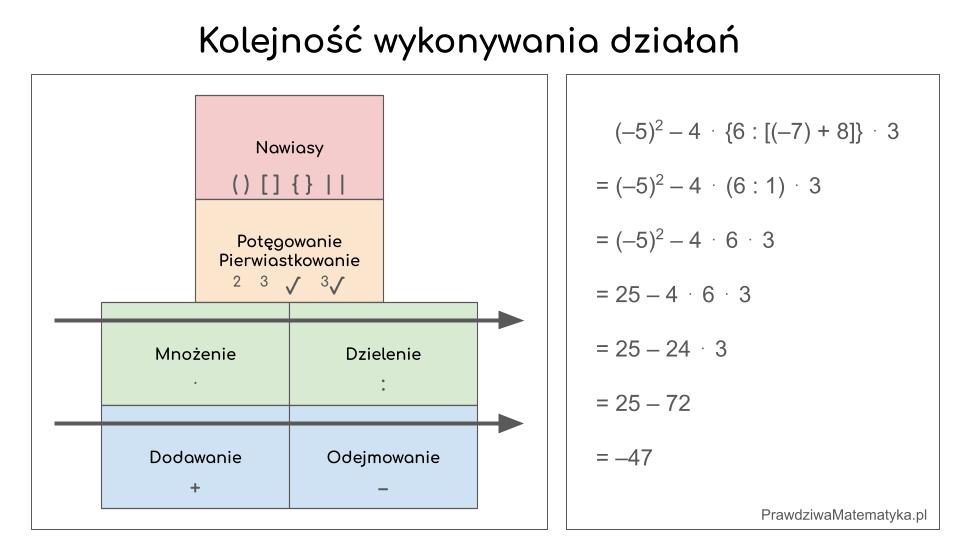
Kolejność wykonywania działań w oparciu o ich hierarchię
Obliczając wartości wyrażeń arytmetycznych kluczowe jest stosowanie się do ściśle określonej kolejności wykonywania działań. Zamiast traktować tę zasadę jako zbiór arbitralnych reguł, proponuję podejście oparte na logicznej hierarchii “mocy” operacji. Zrozumienie tej hierarchii dostarcza intuicyjnego uzasadnienia, dlaczego matematycy umówili się wykonywać niektóre działania przed innymi. Priorytet działań wynika z ich wzajemnej zależności i sposobu, w […]
Kolejność wykonywania działań w oparciu o ich hierarchię Dowiedz się więcej »