Zofia Zielińska-Kolasińska

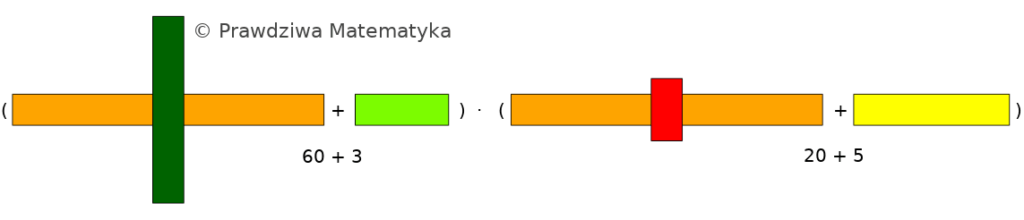
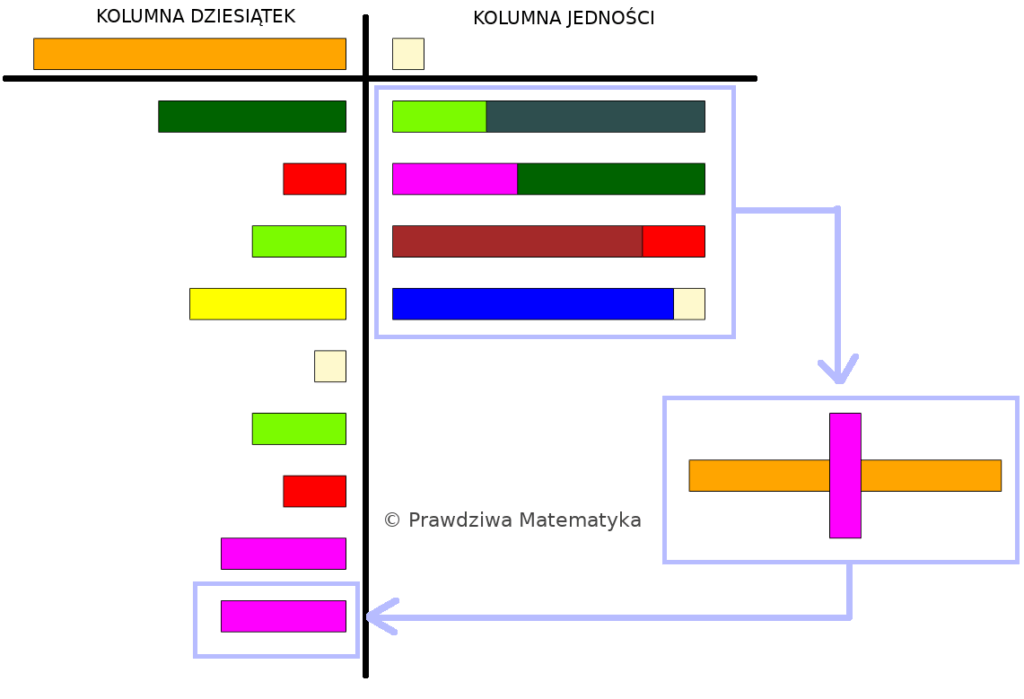
Mnożenie liczb wielocyfrowych – KODOWANIE

Wielu uczniów, a co gorsza także wielu dorosłych, postrzega matematykę jako serię niezależnych od siebie algorytmów. Wystarczy im, że nauczą się kilku wzorów, nabiorą wprawy w stosowaniu kilku procedur i mają poczucie, że nauczyli się matematyki. Nie mają świadomości, że poza biegłością proceduralną jest jeszcze ogromna głębia, którą przeoczyli. Jako nauczyciele wiemy, że to błędna droga. Cel […]

Mnożenie liczb wielocyfrowych – KODOWANIE Dowiedz się więcej »

Sortowanka ZAWSZE, CZASEM, NIGDY wspiera rozumienie ułamków

W pracy z uczniami regularnie napotykam na fundamentalny paradoks: potrafią poprawnie wykonać ciąg skomplikowanych działań na ułamkach, lecz w obliczu pytania teoretycznego ich wiedza zdaje się rozpadać. Problem nie leży w braku umiejętności liczenia, lecz w braku głębokiego zrozumienia pojęć, co w dłuższej perspektywie zamyka drogę do nauki algebry i wyższej matematyki. Z tą myślą,

Sortowanka ZAWSZE, CZASEM, NIGDY wspiera rozumienie ułamków Dowiedz się więcej »

Odcinek S03E02 – Sztuka wizualizacji danych: o wykresach słów kilka (SERIA: ,,A po co mi matma?”)

Opis odcinka Cześć! Nazywam się Zofia i zapraszam Cię do wysłuchania drugiego odcinka trzeciego sezonu podcastu “Prawdziwa Matematyka”! Dziś zajmiemy się światem liczb przedstawionych za pomocą obrazków. — Rozejrzyj się wokół – wykresy, statystyki, dane! Ale czy zawsze rozumiemy, co nam pokazują? I czy liczby potrafią kłamać? Odkryjemy, jakie są podstawowe rodzaje wykresów i do czego

Odcinek S03E02 – Sztuka wizualizacji danych: o wykresach słów kilka (SERIA: ,,A po co mi matma?”) Dowiedz się więcej »

Odcinek S03E01 – Matematyka w kuchni: jak matematyka pomaga gotować i piec z precyzją (SERIA: ,,A po co mi matma?”)

Opis odcinka Cześć! Zapraszam Cię do wysłuchania pierwszego odcinka trzeciego sezonu podcastu “Prawdziwa Matematyka”! Ten sezon to seria “A po co mi matma?”, w której bawimy się w chowanego z matematyką i odkrywamy, gdzie można ją znaleźć w otaczającej nas rzeczywistości. — Dziś przeniesiemy się prosto do serca domu, by udowodnić, że liczby, proporcje i

Odcinek S03E01 – Matematyka w kuchni: jak matematyka pomaga gotować i piec z precyzją (SERIA: ,,A po co mi matma?”) Dowiedz się więcej »

Klocki Cuisenaire’a – rozkład na czynniki pierwsze

W poprzednim artykule odkrywaliśmy liczby parzyste, nieparzyste, pierwsze i złożone za pomocą Klocków Cuisenaire’a. Dziś zanurzymy się głębiej w świat liczb, badając dzielniki oraz fascynujące pojęcie rozkładu na czynniki pierwsze. Klocki pozwolą nam wizualizować te abstrakcyjne idee, budując solidne podstawy dla dalszej nauki matematyki. Przyjmijmy, że biały klocek \(\text{BIA} = 1\). Dzielniki liczby Każdą liczbę

Klocki Cuisenaire’a – rozkład na czynniki pierwsze Dowiedz się więcej »

Klocki Cuisenaire’a – liczby parzyste, nieparzyste, pierwsze i złożone

W świecie Klocków Cuisenaire’a abstrakcyjne pojęcia matematyczne, takie jak liczby parzyste, nieparzyste i pierwsze, nabierają konkretnego, wizualnego kształtu. Dzięki prostym operacjom na klockach, dzieci mogą samodzielnie odkryć i zdefiniować te terminy, co prowadzi do głębszego i bardziej intuicyjnego zrozumienia. Przyjmijmy, że przyjmujemy, że biały klocek \(\text{BIA} = 1\). Definicje w oparciu o klocki Cuisenaire’a Liczba

Klocki Cuisenaire’a – liczby parzyste, nieparzyste, pierwsze i złożone Dowiedz się więcej »

Klocki Cuisenaire’a – mnożenie liczb wielocyfrowych

W poprzednim artykule zgłębialiśmy podstawowe zasady mnożenia i jego kluczowe własności, takie jak przemienność, łączność i rozdzielność. Dziś kontynuujemy naszą podróż, skupiając się na praktycznym zastosowaniu prawa rozdzielności w mnożeniu liczb dwucyfrowych – to właśnie tam metoda iloczynów częściowych staje się niezwykle pomocna. Klocki Cuisenaire’a, choć w bardziej zaawansowanych obliczeniach służą głównie do wizualizacji procesu,

Klocki Cuisenaire’a – mnożenie liczb wielocyfrowych Dowiedz się więcej »

Klocki Cuisenaire’a – mnożenie liczb naturalnych

Kontynuujemy naszą podróż po świecie arytmetyki z Klockami Cuisenaire’a! Po opanowaniu dodawania i odejmowania, nadszedł czas na mnożenie – operację, która bywa dla wielu dzieci (i dorosłych!) bardziej abstrakcyjna. Klocki Cuisenaire’a oferują jednak konkretny sposób na zrozumienie, czym właściwie jest mnożenie i jak działają jego fundamentalne prawa. Przyjmijmy, że biały klocek (BIA) będzie naszą jednostką

Klocki Cuisenaire’a – mnożenie liczb naturalnych Dowiedz się więcej »

Klocki Cuisenaire’a – dodawanie i odejmowanie liczb naturalnych – przekraczanie progu i pożyczanie

W poprzednich artykułach odkrywaliśmy, jak Klocki Cuisenaire’a pomagają zrozumieć podstawowe operacje dodawania i odejmowania, a także fundamentalne własności tych działań. Dziś idziemy o krok dalej i zmierzymy się z arcyważnymi pojęciami w arytmetyce: ,,przekraczaniem progu” w dodawaniu i ,,rozmienianiem” (potocznie, niezbyt szczęśliwie, nazywanym ,,pożyczaniem”) w odejmowaniu. Klocki Cuisenaire’a sprawią, że te abstrakcyjne mechanizmy staną się

Klocki Cuisenaire’a – dodawanie i odejmowanie liczb naturalnych – przekraczanie progu i pożyczanie Dowiedz się więcej »

Przewijanie do góry