Czy Twoje dziecko uczy się w klasie 5 i zaczyna mieć trudności z tematami takimi jak Największy Wspólny Dzielnik (NWD) lub Najmniejsza Wspólna Wielokrotność (NWW)? Czy gubi się w gąszczu cech podzielności?
Ten moduł to solidna, wizualna i praktyczna podstawa do zrozumienia fundamentów teorii liczb, kluczowych na tym etapie edukacji.
Moduł I składa się z 16 lekcji, w tym prawie 5,5 godziny nagranych ćwiczeń!
Co Twoje Dziecko Osiągnie w Tym Module?
Ten moduł to 15 kompleksowych lekcji, które zapewniają pełne opanowanie następujących zagadnień:
- Parzystość i nieparzystość sum i iloczynów: Dziecko zrozumie, dlaczego m.in. ,,parzysta + parzysta = parzysta”, bo zamodeluje te i podobne własności w sposób wizualny, zamiast uczyć się ich na pamięć.
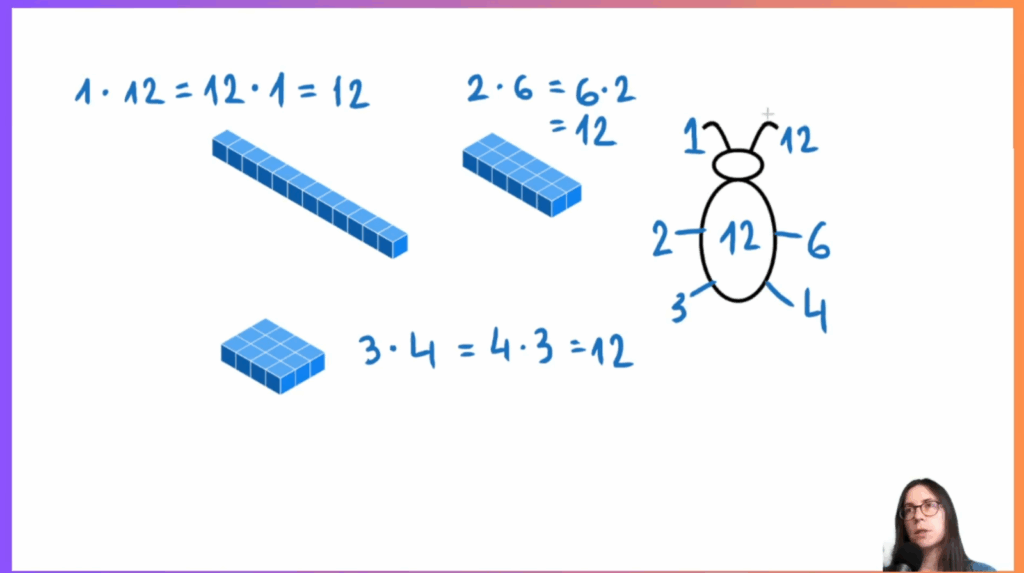
- Liczby pierwsze i złożone: Dziecko nauczy się rozpoznawać te liczby i wizualizować je za pomocą macierzy i pogłębi swoją wiedzę i zrozumienie tematu analizując Sito Eratostenesa.
- Dzielniki i wielokrotności w praktyce (NWD i NWW): Koniec z myleniem dzielnika z wielokrotnością! Wyjaśniamy różnice i pokazujemy, jak wykorzystać te pojęcia do rozwiązywania typowych zadań tekstowych.
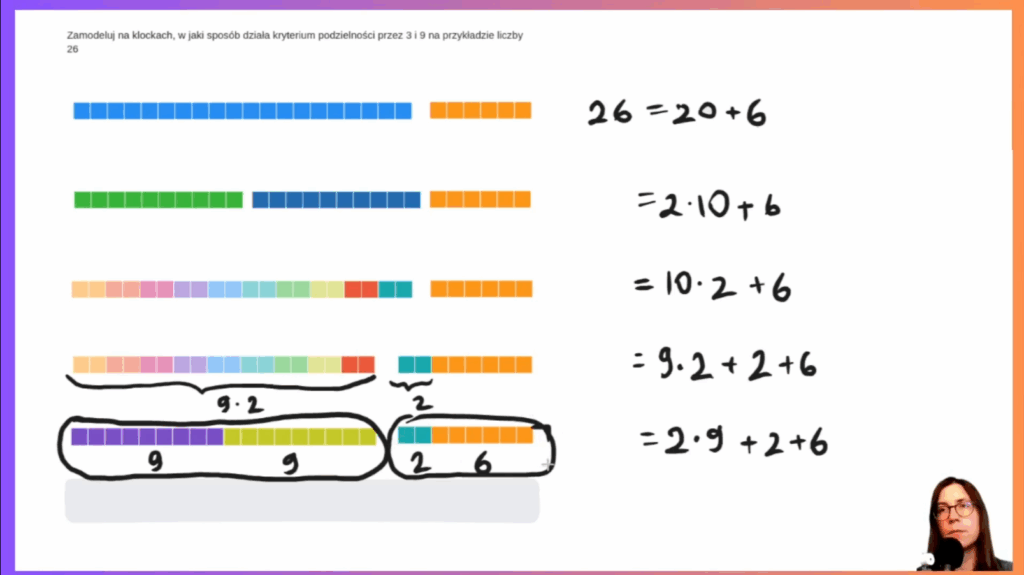
- Kryteria podzielności liczb (2, 3, 4, 5, 8, 9, 10): Uczymy się, jak szybko sprawdzić podzielność liczb bez kalkulatora. Przedstawiamy sens tych reguł (np. skąd bierze się reguła dla 3 i 9), a nie tylko same zasady!
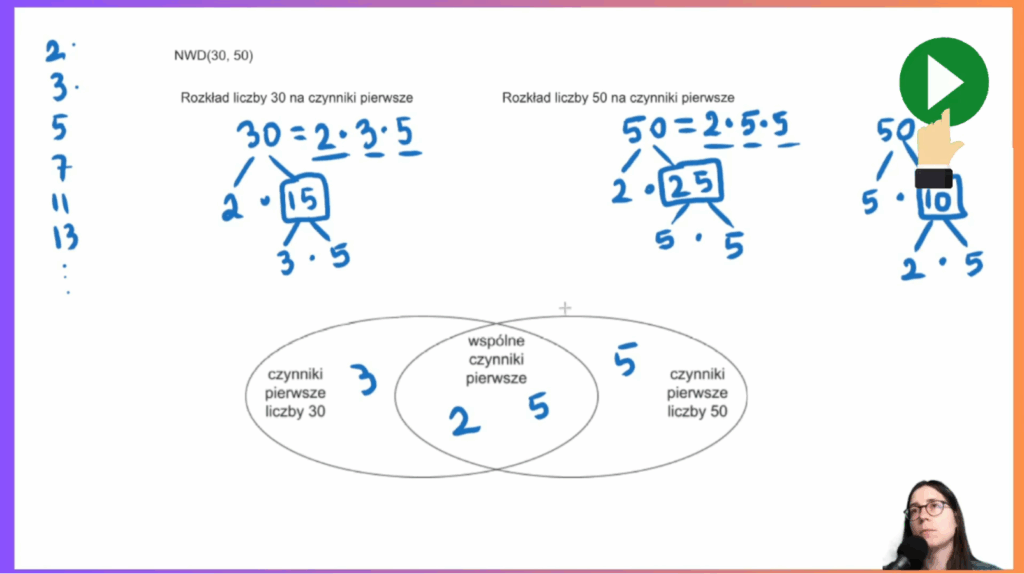
- Rozkład na czynniki pierwsze: Uczymy się budować “drzewka” i wykorzystywać diagramy Venna do obliczania NWD i NWW w oparciu o zrozumienie i bez wkuwania procedur.
- Algorytm Euklidesa: Dziecko pozna ten starożytny algorytm oraz sposób jego wizualizacji w kontekście kafelkowania prostokąta. To najlepszy sposób, aby zrozumieć, w jaki sposób działa ten algorytm i dlaczego otrzymany wynik rzeczywiście jest największym wspólnym dzielnikiem rozpatrywanych liczb!
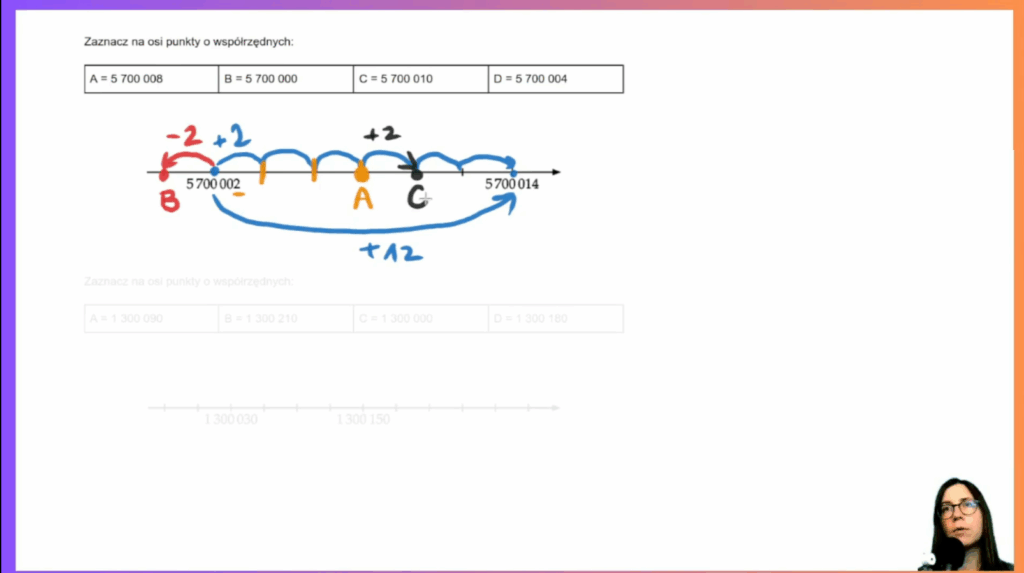
- Odczytywanie i zaznaczanie punktów na osi liczbowej: Przypominamy sobie jak odczytywać współrzędne wskazanego punktu, gdy dane są współrzędne dwóch innych punktów oraz jak zaznaczać na osi punkty o podanych współrzędnych.
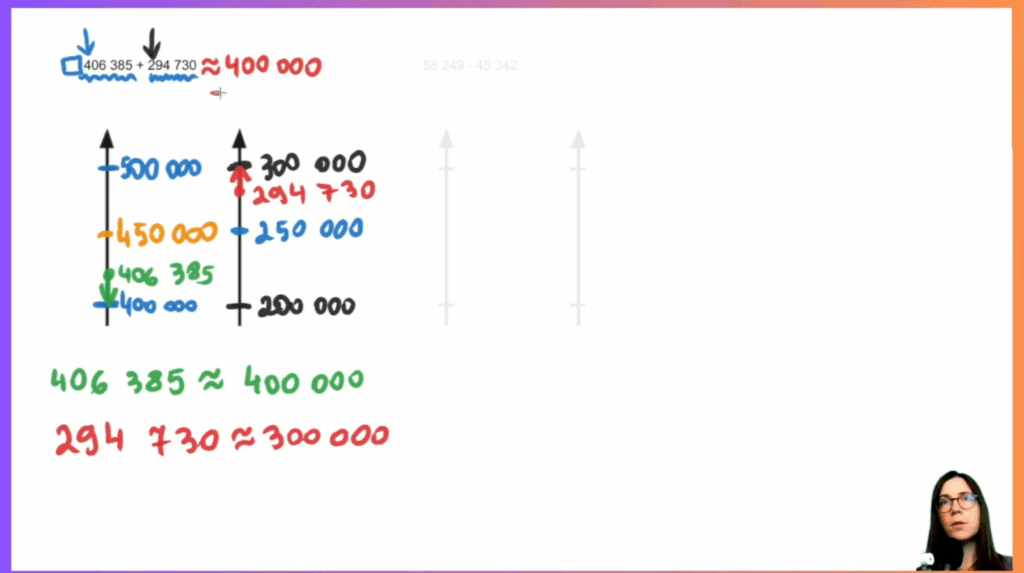
- Zaokrąglanie liczb: Poznajemy zaokrąglanie dużych liczb na osi liczbowej, ucząc się w oparciu o zrozumienie, kiedy zaokrąglać w górę, a kiedy w dół, bez ślepego bazowania na regułce z podręcznika. Uczymy się wykonywać działania przybliżone. Mierzymy się z praktycznymi problemami szacowania liczb, w których nie zawsze należy szacować w sposób oparty o reguły matematyczne.
Dlaczego ten Moduł jest Wyjątkowy?
- Podejście wizualne: Zamiast suchych zapisów matematycznych, używamy pomocy wizualnych, aby abstrakcyjne pojęcia stały się namacalne.
- Wzmocnienie logicznego myślenia: Moduł wprowadza zaawansowane myślenie algorytmiczne poprzez wizualne uzasadnienie Algorytmu Euklidesa (kafelkowanie prostokąta). Zamiast nudnej procedury, dziecko widzi, jak działa ,,logiczna machina”, co rozwija umiejętność rozwiązywania problemów na poziomie, który wykracza poza standardowy program
- Matematyka w życiu codziennym: Tematyka NWD i NWW jest natychmiast przenoszona do praktycznych problemów z życia wziętych (pakowanie paczek, spotkania sportowców, cięcie materiału). Dziecko uczy się, że matematyka nie jest oderwana od rzeczywistości, ale jest narzędziem do rozwiązywania realnych dylematów, co zwiększa motywację do nauki.
Najczęściej zadawane pytania
Dla kogo jest ten moduł?
Moduł jest idealny dla uczniów klasy 5 (lub zdolnych uczniów klasy 4), którzy chcą nadrobić braki lub solidnie przygotować się do dalszej nauki zagadnień z teorii liczb.
Jak upewnić się, że to jest moduł, którego moje dziecko potrzebuje? Czy możemy sprawdzić jego poziom?
Oczywiście! Przed zakupem modułu zachęcamy do rozwiązania krótkiego Testu Diagnostycznego. Ten test zawiera próbkę zadań z zakresu zagadnień, które są omawiane w tym module. Jeśli Twoje dziecko ma problem z większością tych pytań, oznacza to, że ten Moduł będzie dla niego idealnym rozwiązaniem, by solidnie opanować wszystkie zagadnienia.
Ile czasu zajmie przerobienie modułu?
Moduł składa się z 16 lekcji (15 lekcji zawierających nagrania ćwiczeń oraz 1 lekcję zawierającej sprawdzian z całego działu), więc warto przeznaczyć na jego realizację 3-4 tygodnie.
Z czego składa się pojedyncza lekcja i ile trwa?
Pojedyncza lekcja składa się z quizów rozgrzewkowych, nagranych ćwiczeń oraz zadań do samodzielnego rozwiązania i sprawdzenia.
Łączna długość nagranych ćwiczeń to prawie 5,5 godziny, co daje średnio około 21 minut nagrań na lekcję. Przed obejrzeniem nagrań do danej lekcji, należy rozwiązać quizy rozgrzewkowe (około 5 minut), a na koniec rozwiązać samodzielnie zestaw zadań (około 20 minut). Pojedyncza lekcja nie powinna zająć uczniowi więcej, jak 45-50 minut.
Czy są potrzebne jakieś pomoce fizyczne?
Wystarczy kartka, ołówek i ewentualnie małe przedmioty do liczenia (np. fasolki, monety lub klocki) do modelowania, jeśli uczeń woli pracować na fizycznych pomocach, a nie rysować. Uczeń powinien mieć dostęp do drukarki, ponieważ integralną częścią kursu jest zbiór zadań do samodzielnego rozwiązania, które należy wydrukować (lub rozwiązywać na urządzeniu za pomocą rysika).
Czy ten moduł to tylko oglądanie filmów?
Absolutnie nie. Moduł jest interaktywny i wymaga aktywnego udziału.
Na początku każdej lekcji należy rozwiązać quizy rozgrzewkowe, które stanowią krótkie powtórzenie lub wstęp do bieżącej lekcji.
Filmy z ćwiczeniami nagrane są w taki sposób, aby zachęcać ucznia do aktywnego udziału. Nie są one w formie wykładu, ale ćwiczeń, w których co chwila zadawane są uczniowi pytania lub uczeń proszony jest o wykonanie następnego kroku samodzielnie, zanim zostanie zademonstrowane dalsze rozwiązanie.
Każda lekcja kończy się zestawem zadań, które uczeń powinien rozwiązać samodzielnie. Zadania są podobne do ćwiczeń, które znajdowały się na nagraniach, więc w razie wątpliwości uczeń ma możliwość powrotu do nagrań i ponownego obejrzenia fragmentów, których nie udało mu się przyswoić.
Czy ten moduł pomoże w rozwiązywaniu zadań z podręcznika?
Tak! Moduł koncentruje się na zrozumieniu podstaw, co natychmiast przekłada się na lepsze wyniki w zadaniach tekstowych i typowych ćwiczeniach szkolnych dotyczących liczb naturalnych.
Czy uczeń może liczyć na pomoc nauczyciela?
Tak! Zapraszamy na dyżury nauczyciela, które odbywają się w trybie online co najmniej 2 razy w tygodniu.
Jak długo mamy dostęp do materiałów po zakupie?
Dostęp do treści modułu jest przydzielany na 180 dni od daty zakupu. Możecie wielokrotnie wracać do lekcji i ćwiczeń.

