Witaj! Czy ułamki wydają się Twoim uczniom zbyt abstrakcyjne? Ten wpis to zapis kluczowych myśli z mojego webinaru, w którym pokazałam, jak dodawanie i odejmowanie ułamków o tym samym mianowniku może stać się proste i intuicyjne. Zrozumienie to podstawa – bez niego każda kolejna lekcja staje się trudniejsza, a dzieci zniechęcają się do matematyki. Poniżej znajdziesz plan, który pomoże Ci w przygotowaniu lekcji, która buduje solidne podstawy na przyszłość.
Fundamenty, które musisz sprawdzić
Zanim zaczniesz uczyć dodawania i odejmowania ułamków, musisz upewnić się, że Twoi uczniowie mają solidne podstawy. Upewnij się, że dzieci:
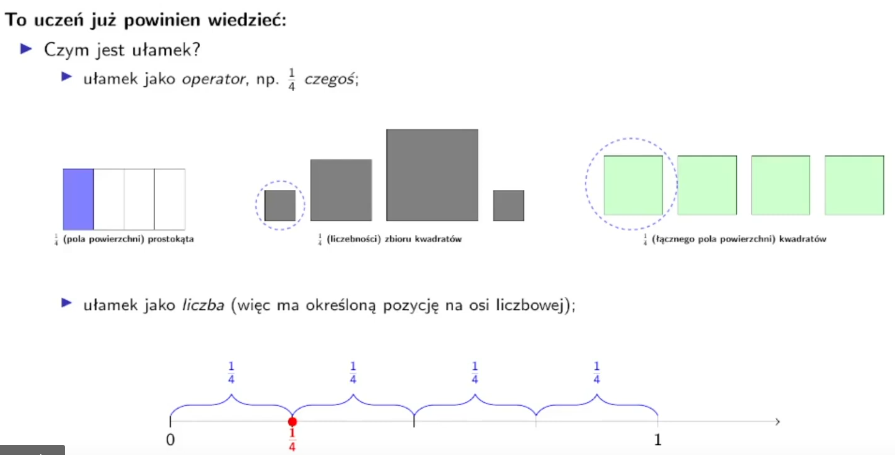
- Rozumieją, czym są ułamki: Potrafią symbolicznie zapisać i przeczytać zarówno ułamki jednostkowe (np. \(1\over4\), jak i niejednostkowe (np. \(3\over4\)). Powinny umieć przedstawiać je na różnych modelach, takich jak paski ułamkowe, koła czy zbiory obiektów.
- Znają pojęcie całości: Wiedzą, że ułamek, którego licznik i mianownik są takie same, reprezentuje jedną całość (np. \(\frac{4}{4} = 1\)). Jest to kluczowe do późniejszego odejmowania ułamków od całości.
- Wiedzą, jak komponować ułamki: Rozumieją, że ułamek \(6\over8\) to suma sześciu ułamków \(1\over8\). Ten koncept jest fundamentalny do zrozumienia, dlaczego w dodawaniu i odejmowaniu ułamków o tym samym mianowniku dodajemy i odejmujemy tylko liczniki.
Główne cele lekcji
W klasie 3 skupiamy się na czterech głównych celach:
- Dziecko potrafi dodać ułamki o tym samym mianowniku.
- Dziecko potrafi odjąć ułamki o tym samym mianowniku.
- Dziecko rozumie, że dodawanie i odejmowanie ułamków są działaniami odwrotnymi.
- Dziecko potrafi odjąć ułamek od całości, zamieniając ją wcześniej na ułamek.
Metodyka: od konkretu do abstrakcji
Moja metoda opiera się na praktycznym podejściu, które odchodzi od suchych regułek.
- Użyj kontekstu: Zaczynaj lekcję od prostych przykładów z życia, np. dzielenie pizzy czy ogrodu. Używaj modeli ciągłych (np. tarcza zegara) i modeli dyskretnych (np. zbiór owoców), aby pokazać ułamek w różnych sytuacjach.
- Wizualizuj: Zachęcaj uczniów do rysowania, używania pasków ułamkowych czy osi liczbowej. To pomaga im zobaczyć, co dzieje się z ułamkami.
- Zachęcaj do mówienia: Poproś uczniów, aby czytali ułamki na dwa sposoby (np. \(2\over6\) i dwie jedne-szóste). To pomoże im zrozumieć strukturę ułamka.
- Użyj błędów do nauki: Pokazuj celowo błędne obliczenia (np. \(\frac{3}{6} + \frac{2}{6} = \frac{5}{12}\)) i proś uczniów, aby wytłumaczyli, dlaczego są one niepoprawne.
- Buduj relacje: Pokaż, że dodawanie i odejmowanie ułamków to działania odwrotne. Poproś ucznów, aby stworzyli wszystkie możliwe działania dla danego zbioru ułamków.
- Odejmowanie od całości: Kiedy przechodzisz do odejmowania ułamków od całości, zacznij od modelu (np. 1 cała pizza), a następnie pokaż, że ta całość może być reprezentowana jako ułamek (np. \(4\over4\)).
Poniżej znajduje się nagranie webinaru, które szczegółowo omawia wszystkie te metody. Życzę miłego i owocnego oglądania!



