Gdy po raz pierwszy widzimy Klocki Cuisenaire’a, często myślimy: ,,Ale słodkie, to na pewno dla przedszkolaków!” 😀 I owszem, są one fantastyczne dla najmłodszych, pomagając im zrozumieć liczby i podstawy arytmetyki. Ale prawda jest taka, że Klocki Cuisenaire’a to narzędzie, które rewolucjonizuje naukę matematyki na każdym etapie – od przedszkola po wyższe klasy.
Dlaczego? Ponieważ, wbrew pozorom, klocki te są konkretne tylko w tym sensie, że można nimi manipulować. W każdym innym aspekcie są niezwykle abstrakcyjne. I właśnie ta abstrakcyjność sprawia, że są genialne.
Do nazywania klocków, będziemy posługiwać się skrótami od pierwszych liter ich kolorów:
- Biały (1 cm): BIA
- Czerwony (2 cm): CZE
- Jasnozielony (3 cm): JZI
- Fioletowy (4 cm): FIO
- Żółty (5 cm): ŻÓŁ
- Ciemnozielony (6 cm): CZI
- Czarny (7 cm): CZA
- Brązowy (8 cm): BRĄ
- Niebieski (9 cm): NIE
- Pomarańczowy (10 cm): POM

Od konkretu do symbolu: początek myślenia algebraicznego
Wyobraź sobie, że pewnego dnia ustalamy, że brązowy klocek reprezentuje wartość \(b\). Wtedy fioletowy klocek będzie jego połową, czyli \(b\over2\).
Innego dnia ten sam brązowy klocek może symbolizować liczbę odpowiadającą jego długości, czyli 8, a fioletowy – 4. Ale niezależnie od przypisanych wartości, jedna relacja pozostaje niezmienna: brązowy klocek jest zawsze dwa razy dłuższy od fioletowego. Możemy to zapisać symbolicznie jako: \(\text{BRĄ} = 2 \cdot \text{FIO}\).
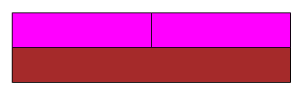
Brązowy: \(8\), fioletowy: \(4\);
\(\text{BRĄ} = 2 \cdot \text{FIO}\)
Ta równość, \(\text{BRĄ} = 2 \cdot \text{FIO}\), jest na dokładnie takim samym poziomie abstrakcji co równanie \(x = 2y\). Przypisywanie wartości liczbowych do brązowego i fioletowego klocka to nic innego jak znajdowanie rozwiązań równania \(x = 2y\). Zamiast więc być “dziecięcą zabawą”, Klocki Cuisenaire’a to świetny wstęp do algebry!
Dlaczego klocki są lepsze od symboli?
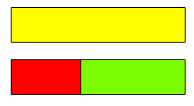
Jedną z największych zalet Klocków Cuisenaire’a jako symboli liczb jest to, że ich długości odzwierciedlają właściwości liczb. Weźmy na przykład cyfrę \(5\). Czy patrząc na nią, widzisz w niej symbol oznaczający sumę liczb \(2\) i \(3\)? Nie, jest to tylko symbol. Ale żółty klocek (\(5\) cm długości) jest w sposób wizualny sumą długości czerwonego (\(2\) cm) i jasnozielonego (\(3\) cm) klocka. Wystarczy ułożyć je obok siebie, by to zobaczyć!
Odkrywanie relacji: równość, nierówność i operacje odwrotne
Dzięki klockom, pojęcia równości i nierówności stają się dziecinnie proste. Łatwo jest zobaczyć, że ,,ten klocek jest dłuższy od tamtego” lub “te dwa klocki są tej samej długości”. Stosunki i proporcje stają się oczywiste. Dzieci na poziomie przedszkolnym mogą wizualnie zrozumieć, że odejmowanie jest operacją odwrotną do dodawania.
Ciągi arytmetyczne i geometryczne stają się proste do skonstruowania i zrozumienia – wystarczy wrócić do naszych ,,schodków”, o których pisałam w poprzednim artykule! Niezależnie od tego, jakie wartości liczbowe przypiszemy klockom i jakie operacje będziemy na nich wykonywać, relacja między ich długościami pozostaje niezmienna. Jeśli klocek BRĄ jest dwa razy dłuższy od klocka FIO, to ich stosunek zawsze wyniesie \(2 : 1\), niezależnie od tego, jakie wartości liczbowej będą reprezentowane przez BRĄ i FIO. Kluczowe jest więc dogłębne zrozumienie tych stałych relacji.
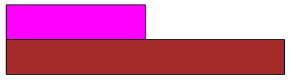
Jeśli klocek FIO reprezentuje wartość \(1\),
to klocek BRĄ reprezentuje wartość \(2\);
jeśli klocek FIO reprezentuje wartość \(25\),
to klocek BRĄ reprezentuje wartość \(50\); itd.
Ćwiczenia, które budują zrozumienie relacji między wielkościami
Aby jak najlepiej poznać relacje między klockami, poświęćcie czas na praktyczne ćwiczenia. Im bardziej zautomatyzowane będzie rozpoznawanie tych zależności, tym łatwiejsze stanie się abstrakcyjne myślenie matematyczne.
Oto kilka pomysłów na ćwiczenia, które możecie wypróbować:

Znajdź klocek, który jest \(3\) razy dłuższy od czerwonego:
\(3 \cdot \text{CZE}= {\Large \text{☐}}\)

Znajdź klocek, który jest dłuższy od żółtego, ale krótszy od czarnego:
\(\text{ŻÓŁ} < {\Large \text{☐}} < \text{CZA}\)
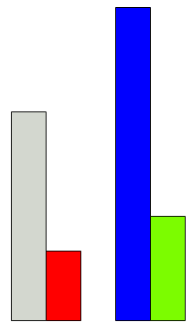
Znajdź klocek, którego długość jest w takiej samej relacji do długości czerwonego klocka, jak długość niebieskiego do długości jasnozielonego:
\(\frac{\huge\text{☐}}{\text{CZE}} = \frac{\text{NIE}}{\text{JZI}}\)
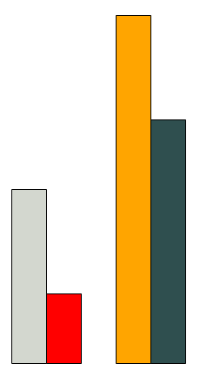
Znajdź klocek, który jest dłuższy od czerwonego o tyle samo, co pomarańczowy jest dłuższy od czarnego:
\({\Large \text{☐}}-\text{CZE} = \text{POM} – \text{CZA}\)
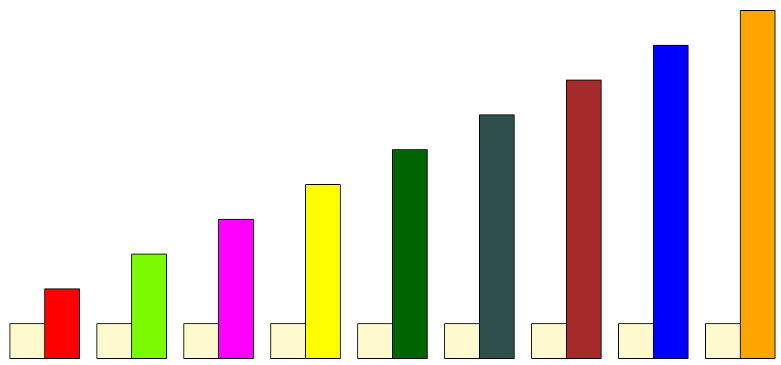
Jakim ułamkiem każdego z pozostałych klocków jest biały klocek?
\(\frac{\text{BIA}}{\text{CZE}} = \frac{1}{2}\)
\(\frac{\text{BIA}}{\text{JZI}} = \frac{1}{3}\)
itd.
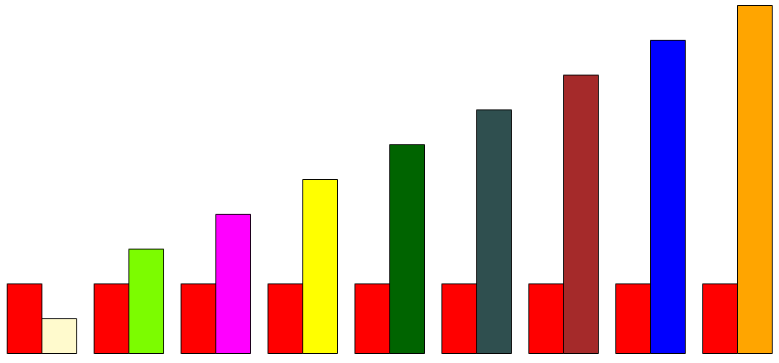
Jakim ułamkiem każdego z pozostałych klocków jest czerwony klocek?
\(\frac{\text{CZE}}{\text{BIA}} = \frac{2}{1} = 2\)
\(\frac{\text{CZE}}{\text{JZI}} = \frac{2}{3}\)
\(\frac{\text{CZE}}{\text{FIO}} = \frac{2}{4}= \frac{1}{2}\)
itd.

Jeśli zbudujesz ,,pociąg” z samych żółtych klocków, a drugi z samych fioletowych klocków, ile klocków musi mieć każdy pociąg, aby były dokładnie tej samej długości?
Czy dałoby się zbudować z czerwonych klocków pociąg tej samej długości?
A z ciemnozielonych?

Czy da się zbudować ,,pociągi” tej samej długości z samych czerwonych i czarnych klocków?
Z jakich innych klocków można zbudować jednokolorowe ,,pociągi” takie, żeby oba miały taką samą długość?
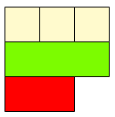
Czy zawsze można zbudować pociąg z czerwonych klocków, który będzie miał taką samą długość jak dowolny inny pociąg?
A z białych klocków?
Jak widać, Klocki Cuisenaire’a to nie tylko kolorowe patyczki, ale potężne narzędzie do rozwijania intuicji matematycznej, myślenia symbolicznego i głębokiego zrozumienia abstrakcyjnych relacji. Nie bójcie się ich używać, eksperymentować i odkrywać – to najlepsza droga do pokochania matematyki!


