Witajcie w kolejnym artykule z naszej serii o wykorzystywaniu Klocków Cuisenaire’a! Jeśli w poprzednich częściach zafascynowała Was ich moc w rozwijaniu wyobraźni przestrzennej, dziś ponownie zanurzymy się w ich równie niezwykłe zastosowanie w świecie arytmetyki i algebry. To właśnie tutaj klocki stają się mostem łączącym abstrakcyjne pojęcia matematyczne z konkretnym, namacalnym doświadczeniem.
Pamiętajcie, że w świecie Klocków Cuisenaire’a, tak jak w każdej grze, istnieją ,,zasady gry”. Są one co prawda arbitralne, ale ich zaletą jest to, że są ustalone i powszechnie stosowane. Dzięki temu, ucząc się z klockami, uczymy się też języka, który pozwoli nam swobodnie komunikować się z innymi, którzy używają tych samych metod. Zamiast widzieć zielony klocek tylko jako 3, nauczymy się, że jest on po prostu ,,jasnozielonym klockiem”, a jego wartość liczbowa może się zmieniać w zależności od tego, jaki klocek przyjmiemy za jednostkę. Takie podejście buduje głębsze zrozumienie relacji liczbowych.
Zatem, przygotujcie swoje klocki! Zaczniemy od samych podstaw dodawania i odejmowania, które są fundamentalne dla dalszych działań matematycznych.
Podstawowe oznaczenia klocków: przypomnienie
Dla przypomnienia, oto podstawowe oznaczenia klocków, które będą nam służyć za ,,nazwy” i ,,wartości” w naszych działaniach:
- Biały (BIA): 1
- Czerwony (CZE): 2
- Jasnozielony (JZI): 3
- Fioletowy (FIO): 4
- Żółty (ŻÓŁ): 5
- Ciemnozielony (CZI): 6
- Czarny (CZA): 7
- Brązowy (BRĄ): 8
- Niebieski (NIE): 9
- Pomarańczowy (POM): 10
Dodawanie klocków: budowanie ,,pociągów”
Zanim przypiszemy klockom konkretne wartości liczbowe, warto najpierw poćwiczyć dodawanie, używając samych nazw kolorów. To pomaga zrozumieć relacje długości, które są stałe, niezależnie od tego, czy biały klocek jest “jedynką”, “połówką” czy “dwusetką”.
Dodawanie z klockami to budowanie ,,pociągów”: Kładziemy klocki koniec do końca, tworząc dłuższą konstrukcję. Następnie szukamy pojedynczego klocka (lub kombinacji, jeśli pociąg jest bardzo długi), który idealnie pasuje do długości naszego pociągu.
Przykład: \[ \text{BIA} + \text{JZI} = \text{CZE}+\text{CZE}=\text{FIO} \]
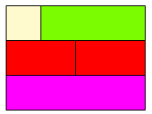
Zauważ, że powyższa relacja pozostaje prawdziwa, nawet jeśli BIA reprezentuje inną wartość niż 1 (np. \( \frac{1}{2} \) lub \(1 234\)). To właśnie siła abstrakcji Klocków Cuisenaire’a!
Tworzenie ,,tkanych dywanów” relacji
Jednym z doskonałych sposobów na ćwiczenie dodawania i poznawania relacji między klockami jest tworzenie ,,tkanego dywanu” wzorów. Polega to na układaniu wszystkich możliwych kombinacji klocków, które mają taką samą łączna długość. To szczególnie praktyczne dla mniejszych klocków.
Przykład: Dla klocka FIO (4) możemy mieć:
- FIO
- JZI + BIA
- BIA + JZI
- CZE + CZE
- CZE + BIA + BIA
- BIA + CZE + BIA
- BIA + BIA + CZE
- BIA + BIA + BIA + BIA
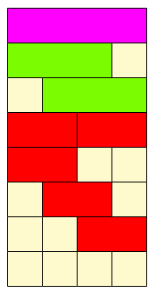
Ćwiczenie: Spróbuj ułożyć wszystkie kombinacje dla klocka ŻÓŁ!
Układanie jednego klocka na wiele sposobów
Dla dłuższych klocków, ciekawym ćwiczeniem jest wyszukiwanie przeróżnych sposobów układania ich jako sumy lub różnice innych klocków.
Przykład: Dla klocka NIE możemy mieć m.in.:
- ŻÓŁ + FIO
- CZI + JZI
- CZA + CZE
- BRĄ + BIA
- FIO + JZI + CZE
- POM – BIA
- (POM + BIA) – CZE
- (POM + ŻÓŁ) – ZIE
- (ŻÓŁ + JZI + BIA + FIO) – FIO

Związek między dodawaniem i odejmowaniem
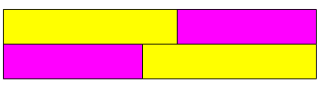
Relacja między dodawaniem a odejmowaniem jest najlepiej widoczna, gdy próbujemy odczytać wszystkie możliwe działania z dwóch ,,pociągów” o tej samej długości.
Patrząc na układ klocków można zaobserwować następujące działania:
- NIE = ŻÓŁ + FIO
- NIE = FIO + ŻÓŁ
- NIE – FIO = ŻÓŁ
- NIE – ŻÓŁ = FIO
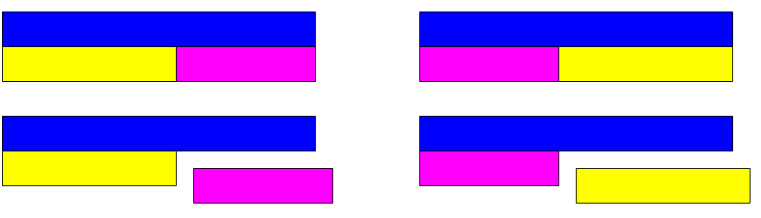
Zmieniając położenie ,,pociągów”, można zaobserwować także przemienność dodawania:
ŻÓŁ + FIO = FIO + ŻÓŁ
Prawo łączności dodawania
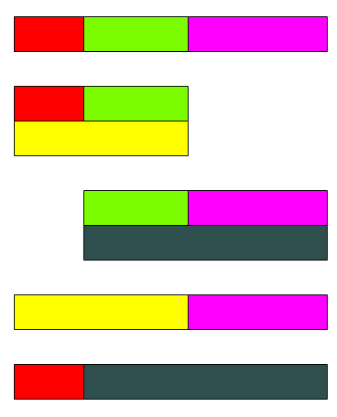
Prawo łączności dodawania, czyli fakt, że kolejność grupowania liczb w dodawaniu nie ma znaczenia, staje się oczywiste, gdy budujemy ,,pociągi” z trzech klocków, a następnie grupujemy je na różne sposoby.
- Rozważmy działanie:
CZE + JZI + FIO - Najpierw sumujemy dwa pierwsze składniki:
CZE + JZI = ŻÓŁ - Następnie sumujemy dwa dalsze składniki:
JZI + FIO = CZA - Jak widać, zachodzi równość sum, tj. suma dwóch pierwszych składników powiększona o trzeci jest taka sama, jak suma dwóch dalszych składników powiększona o pierwszy:
(CZE + JZI) + FIO = CZE + (JZI + FIO)
Dodawanie w zakresie 20
Gdy zaczynamy naukę dodawania liczb naturalnych, najwygodniej jest użyć białego klocka (BIA) jako jednostki \(1\).
Kombinacje do \(10\): Aby zrozumieć kombinacje dające \(10\), bardzo pomocne jest ułożenie dwóch ,,schodów” z klocków, jeden w normalnej kolejności, drugi w odwróconej, i dopasowanie ich tak, aby sumowały się do długości pomarańczowego klocka (10).
Przykład ,,schodów do 10″: Jeśli \(\text{BIA} = 1\):
- BIA + NIE = POM
(\(1 + 9 = 10\)) - CZE + BRĄ = POM
(\(2 + 8 = 10\)) - JZI + CZA = POM
(\(3 + 7 = 10\)) - FIO + CZI = POM
(\(4 + 6 = 10\)) - ŻÓŁ + ŻÓŁ = POM
(\(5 + 5 = 10\)) - CZI + FIO = POM
(\(6 + 4=10\)) - CZA + JZI = POM
\(7+3=10\)) - BRĄ + CZE = POM
(\(8+2=10\)) - NIE + BIA = POM
(\(9+1=10\))

Kombinacje do \(20\): Gdy już opanujemy kombinacje do \(10\), z łatwością przejdziemy do liczb z zakresu od \(11\) do (20). Każda liczba z tego zakresu może być postrzegana jako jeden pomarańczowy klocek (\(10\)) plus jeden z mniejszych klocków.
- \(11 = \text{POM} + \text{BIA}\)
- \(12 = \text{POM} + \text{CZE}\)
- \(13 = \text{POM} + \text{JZI}\)
- …i tak dalej, aż do \(20 = \text{POM} + \text{POM}\).
Aby to zwizualizować, możemy znowu wykorzystać nasze ,,schodki” z klocków. Przesunięcie dwóch ułożonych schodków (tych, które sumowały się do \(10\)) do nowej pozycji może pokazać kombinacje sumujące się do \(11\).

Przesunięcie ich o kolejny ,,krok” w przód pokaże kombinacje sumujące się do \(12\), i tak dalej. To wspaniały sposób na wizualne odkrywanie i utrwalanie relacji liczbowych wykraczających poza podstawowe dziesięć!

System dziesiętny
Kiedy pracujemy z liczbami większymi niż \(9\), potrzebujemy więcej niż jednej cyfry. W klockach Cuisenaire’a pomarańczowy klocek (POM) może symbolizować \(10\), ponieważ nie ma klocka, który reprezentuje wartość \(0\). Liczby większe od \(10\) są reprezentowane przez kombinacje pomarańczowych klocków i pojedynczego, mniejszego klocka.
Ważna zasada: Pracując w systemie dziesiętnym z klockami, nigdy nie będziemy mieć więcej niż jednego klocka innego koloru niż pomarańczowy. Liczba pomarańczowych klocków będzie cyfrą w kolumnie dziesiątek, a mniejszy klocek cyfrą w kolumnie jedności.
Opierając się na powyższej zasadzie, zawsze musimy wymienić ,,pociąg” ułożony z różnych klocków na równy mu, ale taki, który ma tylko jeden klocek krótszy od pomarańczowego.
Przykład: \[ \text{FIO} + \text{JZI} + \text{CZA} + \text{ŻÓŁ} + \text{CZI} \] \[\text{Jeżeli BIA }=1:\]\[4 + 3 + 7 + 5 + 6 = 10 + 10 + 5 \]\[= 2 \text{ dziesiątki } + 5 \text{ jedności } \]\[= 25\]

Jak to zrobić za pomocą klocków:
- Sposób I:
- Ułóż ,,pociąg” z klocków.
- Układaj poniżej tyle klocków POM, ile zmieści się w ,,pociągu”.
- Uzupełnij ,,pociąg” pasującym, brakującym klockiem.
- Sposób II:
- Zastąp dłuższe fragmenty pociągu pomarańczowymi klockami.
- \( \text{JZI} + \text{CZA} = \text{POM}\) (czyli \(3+7=10\)).
- \( \text{FIO} + \text{CZI} = \text{POM} \) (czyli \(4+6=10\)).
- Pozostaw klocek, krótszy od POM, którego nie udało się zamienić.
- Zastąp dłuższe fragmenty pociągu pomarańczowymi klockami.

Odejmowanie
Zobaczmy, jak możemy myśleć o odejmowaniu na przykładzie działania \(23-7\). Zacznij od ułożenia \(23\) jako \( \text{POM} + \text{POM} + \text{JZI} \), a następnie ułóż poniżej klocek CZA.
Myśląc o odejmowaniu możemy zadać sobie pytanie: ,,co zostanie, gdy od \(23\) zabierzemy \(7\)?” lub jeszcze lepiej: ,,co trzeba dodać do \(7\) żeby otrzymać \(23\)?”, co bardzo łatwo pokazać na klockach.

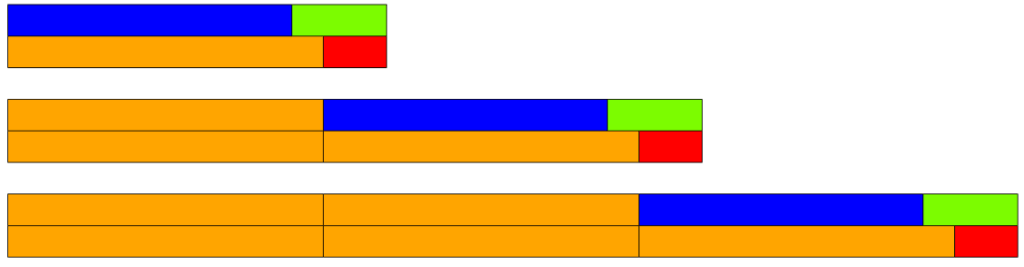
Stała suma
Klocki Cuisenaire’a doskonale demonstrują, że dodawanie takiej samej wielkości do obu stron równości pozwala zachować równość. Jeśli zaczniemy od dwóch ,,pociągów” o takiej samej długości i dodamy do obu taki sam klocek, ich długości nadal będą równe.
Przykład: Jeśli NIE + JZI = POM + CZE: \[ 9 + 3 = 12, \] to dodając do obu stron po \(10\) (klocek POM) nadal mamy zachowaną równość: \[ (\text{POM}+9) + 3 = 12 + \text{POM} \] \[ 19 + 3 = 22 \] i dalej podobnie: \[ (\text{POM}+19) + 3 = 22 + \text{POM} \] \[ 29 + 3 = 32 \] itd.
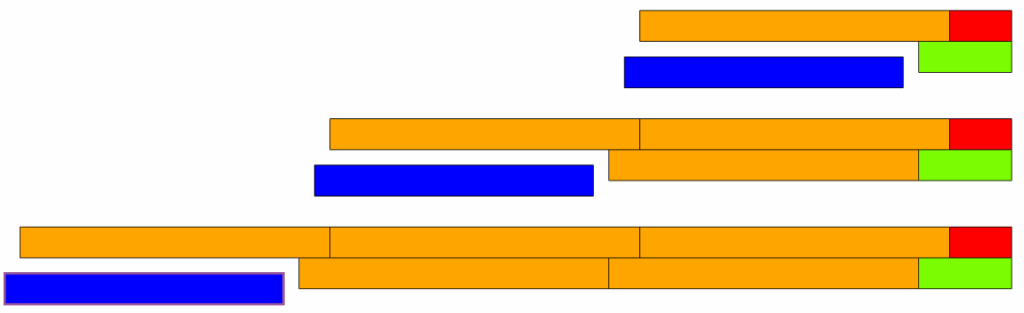
Stała różnica
Analogicznie jak wyżej, rozpatrując działanie odejmowania, jeśli dodamy (lub odejmiemy) taki sam klocek do odjemnej i odjemnika, równość także zostanie zachowana.
Przykład: Przyjrzyj się sekwencji: \[ 12 – 3 = 9 \] \[ 22 – 13 = 9 \] \[ 32 – 23 = 9 \]
Warto rozważyć z dziećmi pytania takie jak: ,,co można dodać (lub odjąć) do odjemnej i odjemnika, aby wynik pozostał niezmieniony?”
Przykład: Skoro \[ \text{CZA} – \text{JZI} = \text{FIO}, \] to również \[ (\text{CZA} + {\large \text{☐}}) – (\text{JZI}+ {\large \text{☐}}) = \text{FIO} \] oraz \[ (\text{CZA} – {\large \text{☐}}) – (\text{JZI}- {\large \text{☐}}) = \text{FIO}. \]
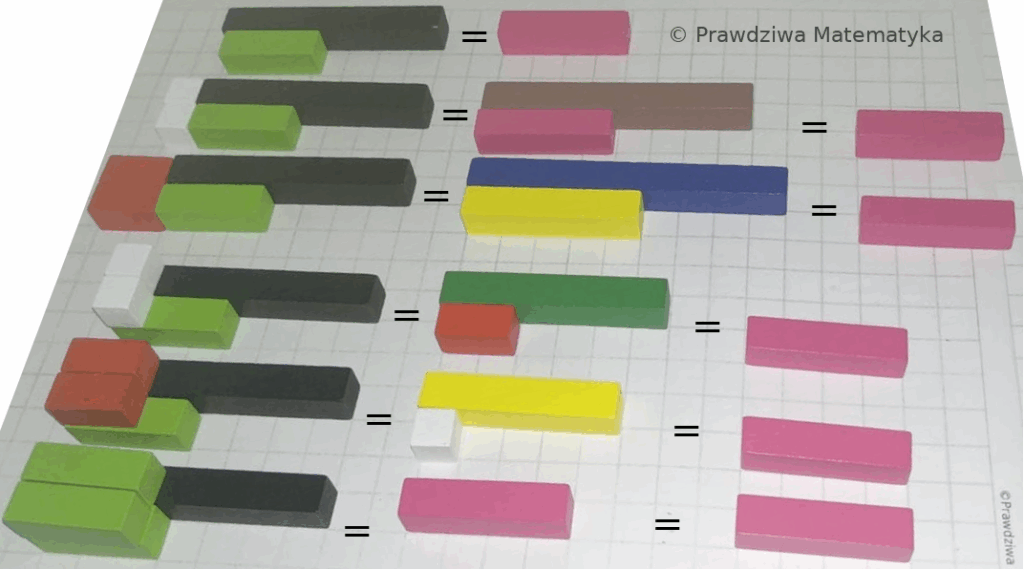
Obserwacja, że różnica pozostaje stała także wtedy, gdy dodamy (lub odejmiemy) taką samą wartość od odjemnej i odjemnika jest bardzo praktyczna przy sprytnym wykonywaniu obliczeń.
Przykład: Działanie \(43-7\) może wydawać się trudne, ale daje się je znacznie uprościć tak: \[(43-3)-(7-3)=40-4=36\] lub tak: \[(43+3)-(7+3)=46-10=36.\]
Co się dzieje, gdy zmienia się tylko odjemna lub odjemnik?
Obserwując, co dzieje się, gdy zmieniamy tylko jedną z wielkości w działaniu odejmowania, można dokonać przydatnych odkryć!
Przykład: Rozważmy działanie \((\text{CZA} – \text{JZI} = \text{FIO})\): \[ 7 – 3 = 4. \]
- Jeśli zwiększymy odjemną, różnica wzrośnie o tyle samo:
- wzrost odjemnej o \(1\): \[ (7+1) – 3 = 4+1\]
- wzrost odjemnej o \(2\): \[ (7+2) – 3 = 4+2 \]

- Jeśli zmniejszymy odjemną, różnica zmaleje o tyle samo:
- spadek odjemnej o \(1\): \[ (7-1) – 3 = 4-1 \]
- spadek odjemnej o \(2\): \[ (7-2) – 3 = 4-2 \]

- Jeśli zwiększymy odjemnik, różnica zmaleje o tyle samo:
- wzrost odjemnika o \(1\): \[ 7 – (3+1) = 4-1 \]
- wzrost odjemnika o \(2\): \[ 7 – (3+2) = 4-2 \]

- Jeśli zmniejszymy odjemnik, różnica wzrośnie o tyle samo:
- spadek odjemnika o \(1\): \[ 7 – (3-1) = 4+1 \]
- spadek odjemnika o \(2\): \[ 7 – (3-2) = 4+2 \]

Klocki Cuisenaire’a to nie tylko kolorowe patyczki, ale potężne narzędzie do budowania solidnych podstaw arytmetyki i algebry. Pozwalają one na konkretne doświadczanie abstrakcyjnych relacji, co jest kluczowe dla głębokiego zrozumienia matematyki. Zanurzcie się w świat klocków i odkryjcie, jak intuicyjne może być dodawanie i odejmowanie! 🙂


