W poprzednich artykułach odkrywaliśmy, jak Klocki Cuisenaire’a pomagają zrozumieć podstawowe operacje dodawania i odejmowania, a także fundamentalne własności tych działań. Dziś idziemy o krok dalej i zmierzymy się z arcyważnymi pojęciami w arytmetyce: ,,przekraczaniem progu” w dodawaniu i ,,rozmienianiem” (potocznie, niezbyt szczęśliwie, nazywanym ,,pożyczaniem”) w odejmowaniu. Klocki Cuisenaire’a sprawią, że te abstrakcyjne mechanizmy staną się namacalne i zrozumiałe!
Pamiętajmy, że bazujemy na założeniu, że biały klocek (BIA) to nasza jednostka (\(1\)), a pomarańczowy klocek (POM) reprezentuje \(10\).
Łączność dodawania
Ćwiczenie: Wybierz klocki o trzech różnych długościach i stwórz z nich wszystkie możliwe pary. Odczytaj utworzone sumy najpierw nazywając kolory klocków, a następnie nadając im wartości liczbowe (przyjmując, że \(\text{BIA}=1\)).
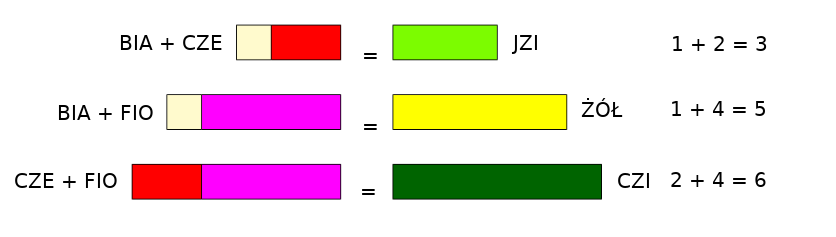
Do każdej sumy dołóż niewykorzystany klocek i upewnij się, że otrzymane w ten sposób ,,pociągi” są takiej samej długości.
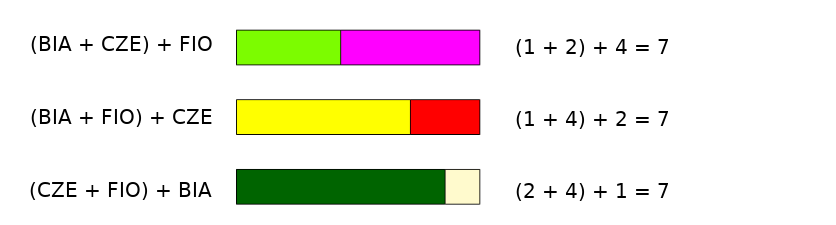
Fakt, że otrzymane ,,pociągi” są tak samo długie świadczy o tym, że nie ma znaczenia w jakiej kolejności dodajemy liczby. Tę własność dodawania nazywamy łącznością.
Łączności dodawania a ,,przekraczanie progu”
Wyobraźmy sobie dodawanie ciągu liczb, na przykład: \[7 + 4 + 5 + 3 + 2 + 6 + 5 + 8.\] Zamiast sumować wszystko po kolei, dużo łatwiej jest szukać par lub grup klocków, które sumują się do \(10\) (czyli do długości pomarańczowego klocka).
Przekonaliśmy się już, że dodawanie jest łączne, a zatem kolejność w jakiej będziemy dodawać liczby nie wpłynie na wynik dodawania. Poszukajmy zatem par liczb sumujących się do \(10\):
- \(7 + 3 = 10\)
(\(\text{CZA} + \text{JZI} = \text{POM}\)) - \(4 + 6 = 10\)
(\(\text{FIO} + \text{CZI} = \text{POM}\)) - \(5 + 5 = 10\)
(\(\text{ŻÓŁ} + \text{ŻÓŁ} = \text{POM}\)) - \(2 + 8 = 10\)
(\(\text{CZE} + \text{BRĄ} = \text{POM}\))

Widzimy, że wszystkie te liczby sumują się łącznie do czterech dziesiątek, czyli \(4 \cdot \text{POM}\), co daje nam wartość \(40\).
Dodawanie kolumnowe liczb dwucyfrowych, czyli ,,przekraczanie progu” w praktyce
Teraz przejdźmy do bardziej złożonego przykładu dodawania kolumnowego, gdzie ,,przekraczanie progu” odgrywa bardzo ważną rolę.
Ćwiczenie: Obliczymy sumę poniższego zestawu liczb dwucyfrowych:
63
24
38
59
11
37
26
+ 42
----
Aby zwizualizować to działanie za pomocą klocków, najpierw musimy zrozumieć, że np. liczba \(63\) oznacza sześć dziesiątek i trzy jedności. Żeby pokazać tę liczbę, powinniśmy ułożyć ,,pociąg” złożony z sześciu klocków POM i trzech klocków BIA. Takie modelownie liczb nie byłoby jednak zbyt praktyczne, bo liczby zajmowałyby bardzo dużo miejsca, a poza tym istniałoby ryzyko, że… zabrakłoby nam klocków!
Umówmy się, że stworzymy w naszej przestrzeni roboczej kolumny odpowiadające poszczególnym rzędom wielkości, a oznaczymy je klockami: lewą kolumnę oznaczymy klockiem POM (co będzie oznaczało dziesiątki), a prawą klockiem BIA (jedności).
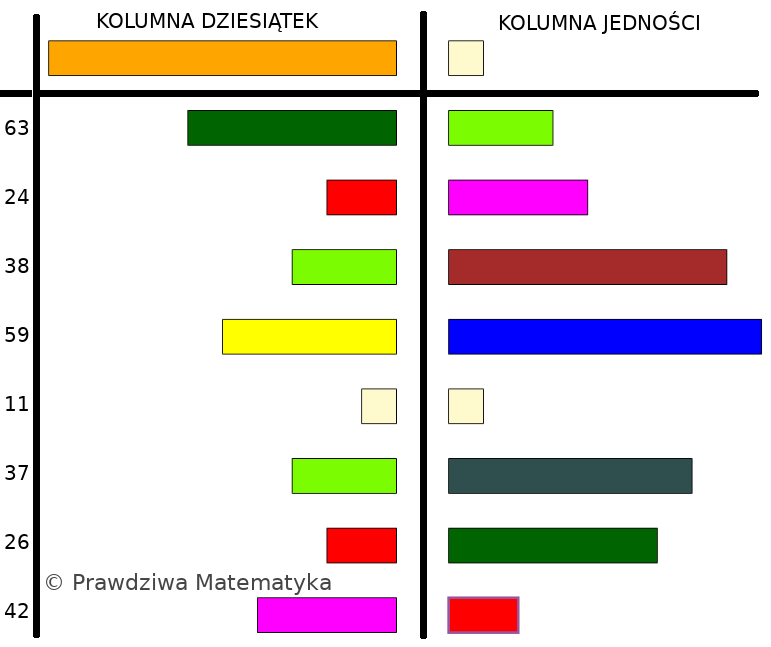
Zgadzamy się, że każdy klocek w kolumnie jedności reprezentuje swoją wartość, a każdy klocek w kolumnie dziesiątek oznacza swoją wartość pomnożoną przez \(10\). Układamy wszystkie składniki naszej sumy zgodnie z powyższymi ustaleniami.
Obliczanie sumy zaczynamy od kolumny jedności. Zbieramy wszystkie klocki reprezentujące jedności: \(3, 4, 8, 9, 1, 7, 6, 2\) i grupujemy je w dziesiątki, czyli układamy w ,,pociągi”, każdy o długości jednego klocka POM.
Po zsumowaniu jedności okazuje się, że otrzymujemy cztery klocki POM.
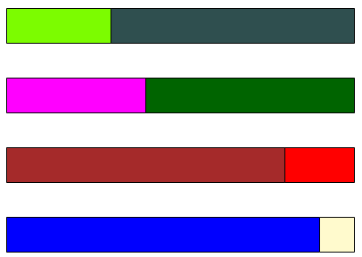
Widzimy zatem, że w kolumnie jedności znajdują się cztery dziesiątki, co możemy ułożyć za pomocą klocków w następujący sposób (konwencję dla mnożenia omówiłam krótko tutaj):
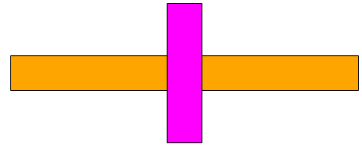
W powyższym układzie, fioletowy klocek oznacza liczbę dziesiątek, które udało nam się stworzyć z klocków z kolumny jedności.
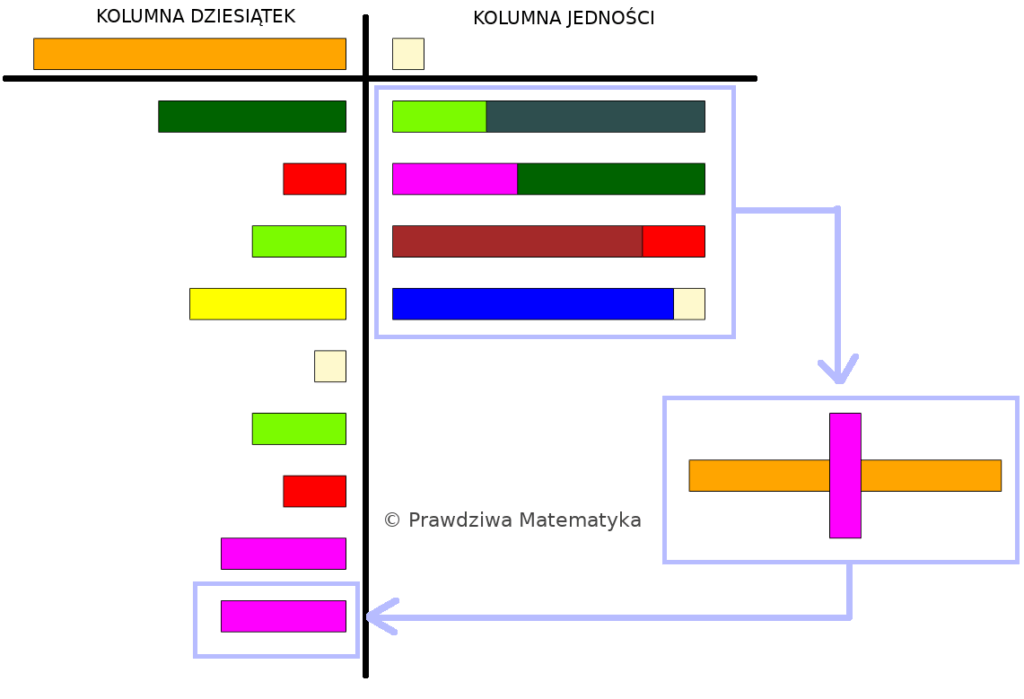
\(40\) jedności to tyle samo, co \(4\) dziesiątki, a zatem przenosimy fioletowy klocek do kolumny dziesiątek, zwiększając tym samym liczbę dziesiątek w tej kolumnie o \(4\). Kolumna jedności jest pusta.
Teraz wykonujemy dodawanie w kolumnie dziesiątek: \(6, 2, 3, 5, 1, 3, 2, 4, 4\). Ostatnia z wypisanych czwórek to ta, która została ,,przeniesiona” z kolumny jedności. Sumujemy liczby, grupując je w zestawy po \(10\):
- \(6+4=10\)
- \(2+3+5=10\)
- \(1+3+2+4=10\)

Mamy dokładnie trzy dziesiątki w kolumnie dziesiątek, czyli \(3\cdot\text{POM}\cdot\text{POM}\), a zatem przenosimy do kolumny setek klocek JZI, który reprezentuje wartość \(3\). Wynik dodawania możemy zapisać w postaci schematycznych tabelek:
POM x POM | POM | BIA 100 | 10 | 1
----------|-----|----- lub -----|----|----
JZI | - | - 3 | 0 | 0Odejmowanie liczb bliskich \(10\)
Działania dodawania i odejmowania powinny być nauczane jednocześnie, żeby dzieci miały świadomość, że na przykład \(12-5=7\), bo \(7+5=12\).
Warto też, mówiąc o odejmowaniu, nie skupiać się wyłącznie na odejmowaniu interpretowanym jako zabieranie: ,,co zostanie, gdy zabiorę 5 od 12?”, ale także jako różnica: ,,co muszę dodać do 5, żeby otrzymać 12?”.
Warto wykorzystać Klocki Cuisenaire’a do wsparcia dzieci w przyswojeniu sprytnej i bardzo efektywnej strategii obliczania różnicy, gdy odjemnik jest bliski \(10\).
- Odejmowanie liczby \(9\):
- \(12-9 = 2 + 1\)
- \(15-9 = 5 + 1\)
- \(17-9=7+1\)
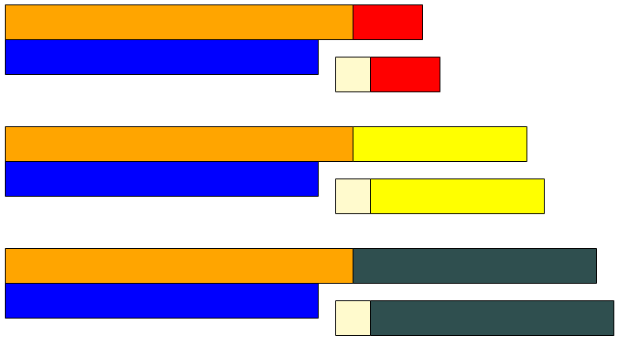
- Odejmowanie liczby \(8\):
- \(12-8 = 2 + 2\)
- \(15-8 = 5 + 2\)
- \(17-8=7+2\)
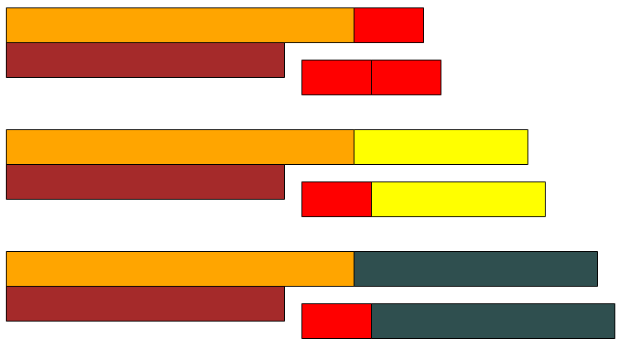
Można wyrazić tę strategię następująco:
,,Bądź zachłanny! Zamiast odejmować 9, odejmij więcej, bo aż 10, a później oddaj nadmiarowe 1.“
Odejmowanie: ,,rozmienianie” zamiast ,,pożyczania”
Termin ,,pożyczanie” w odejmowaniu często wprowadza w błąd, sugerując, że skoro coś pożyczamy, to potem będziemy to oddawać. W rzeczywistości to, co robimy, to ,,rozmienianie” liczby na mniejsze jednostki, co ma na celu ułatwienie wykonania jakiejś operacji.
Ćwiczenie: Obliczymy działanie \[23 – 7.\] Układamy działanie za pomocą klocków:

Ważna uwaga: Dodając i odejmując musimy pamiętać, żeby zawsze wykonywać działania na jednostkach takiego samego typu, np.: \[3 \text{ koty} + 2 \text{ koty} = 5 \text{ kotów},\]\[9 zł – 4 zł = 5 zł.\] Nie możemy dodawać, ani odejmować obiektów różnych typów, np.: \[3 \text{ koty} + 2 \text{ psy} = ???,\]\[9 zł – 4 gr = ???.\] W przypadku, gdy w działaniu występują obiekty wyrażone w różnych jednostkach, zanim wykonamy dodawanie lub odejmowanie, musimy wyrazić wszystkie obiekty jako obiekty tego samego typu, np.: \[3 \text{ koty} + 2 \text{ psy} = 3 \text{ zwierzęta} + 2 \text{ zwierzęta} = 5 \text{ zwierząt},\]\[9 zł – 4 gr = 900 gr – 4 gr = 996 gr.\]
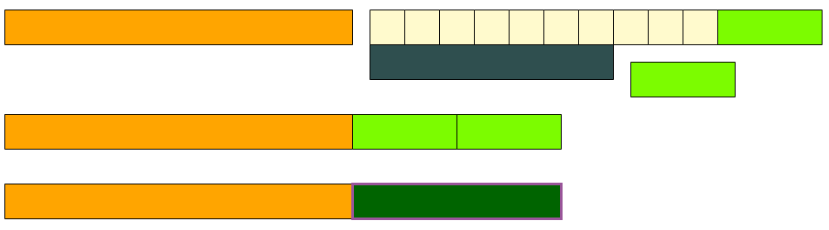
Wróćmy do naszego działania: \(23-7\). W tym działaniu mamy \(2\) dziesiątki i \(3\) jedności, a chcemy odjąć \(7\) jedności. Możemy zapisać to działanie w postaci z jednostkami w następujący sposób: \[2 \text{ dziesiątki} + 3 \text{ jedności} – 7 \text{ jedności}.\]
Jak widać, mamy za mało jedności, żeby wykonać odejmowanie! W takim przypadku wykorzystujemy ,,rozmienianie”, które polega na tym, że \(1\) dziesiątkę ,,rozmieniamy”, tj. ,,wymieniamy” na \(10\) jedności. Nasze działanie wygląda teraz następująco: \[1 \text{ dziesiątka} + 13 \text{ jedności} – 7 \text{ jedności}.\]

Patrząc na działanie zwizualizowane za pomocą klocków widać, że po wykonaniu odejmowania klocka CZA, zostanie 1 klocek POM oraz 6 klocków BIA, a zatem wynikiem działania jest \[1 \text{ dziesiątka} + 6 \text{ jedności} = 16.\]
Odejmowanie można wykonać szybciej, jeśli zna się ,,pary do \(10\)”, czyli wie się z góry, że po wykonaniu odejmowania klocka CZA od klocka POM pozostaje klocek JZI. Wówczas otrzymujemy \[10 + 3 + 3 = 10 + 6 = 16.\]
Odejmowanie dużych liczb: ,,rozmieniamy” setki i dziesiątki
Mechanizm ,,rozmieniania” jest jeszcze bardziej widoczny przy odejmowaniu większych liczb w zapisie kolumnowym.
Ćwiczenie: Rozważmy działanie: \[645 – 497.\]Przygotowujemy w naszej przestrzeni roboczej trzy kolumny rzędów wielkości: setki (\( \text{POM} \cdot \text{POM} \)), dziesiątki (POM) i jedności (BIA) i układamy odjemną oraz odjemnik:

Zanim zaczniemy wykonywać odejmowanie, musimy upewnić się, że w każdej kolumnie jest ono możliwe do wykonania. Jest? Nie! Problem występuje zarówno w kolumnie dziesiątek, jak i jedności, co można poznać po tym, że w każdej z tych kolumn odjemna jest większa od odjemnika. A zatem musimy ,,rozmienić” jedną setkę na \(10\) dziesiątek oraz jedną dziesiątkę na \(10\) jedności. Wartość odjemnej nie zmienia się, zmienia się jedynie postać, w jakiej jest ona zapisana: \[6 \text{ setek} + 4 \text{ dziesiątki} + 5 \text{ jedności}\]\[=5 \text{ setek} + 14 \text{ dziesiątek} + 5 \text{ jedności}\]\[=5 \text{ setek} + 13 \text{ dziesiątek} + 15 \text{ jedności}.\]

Teraz możemy już wykonać odejmowanie w każdej z kolumn, co możemy zapisać następująco:
500 + 130 + 15
-(400 + 90 + 7)
------------------
100 + 40 + 8 = 148Sprytne ,,rozbijanie”
Nie zawsze tradycyjne algorytmy dodawania i odejmowania są najbardziej efektywnymi strategiami wykonywania obliczeń. Warto ćwiczyć elastyczne ,,rozbijanie” liczb tak, aby umieć dobrać odpowiedni sposób postępowania do konkretnego działania, z którym się mierzymy.
Przykład I:
Oblicz sumę: \[395+56.\]
Zapisujemy składniki w innej postaci:\[395 = 400-5,\]\[56=50+6.\]
Wykonujemy dodawanie: \[395+56=(400-5) + (50+6) \]\[= (400+50) + (6-5) = 450 + 1 = 451.\]
Przykład II:
Oblicz różnicę: \[395-56.\]
Zapisujemy odjemną i odjemnik jak wcześniej, a następnie wykonujemy odejmowanie: \[395-56=(400-5) – (50+6) \]\[= 400-50 -5 -6 = 350 – 11 = 339.\]
Sprytne dodawanie
Klocki Cuisenaire’a uczą nas elastyczności, która przekłada się na umiejętność szybkiego szacowania. Rozważmy przykład dodawania, w którym ,,rozbijamy” liczby w sposób elastyczny, aby ułatwić sobie sumowanie:
Przykład: Oblicz sumę, zamieniając składniki w sprytny sposób na sumy i różnice:
396 ---> 400 - 4
412 ---> 400 + 12
593 ---> 600 - 7
+ 736 ---> 700 + 36
---------------------Sumując same pełne setki, otrzymujemy oszacowanie sumy: \(2\ 100\). Następnie zauważamy, że liczby \(-4\) i \(-7\) ,,skasują” prawie całą wartość liczby \(12\), pozostawiając tylko jedną jedynkę. A zatem dokładną wartość sumy obliczymy jako \[2 100 + 1 + 36 = 2 137.\]
Sprytne odejmowanie
W poprzednim artykule zwróciłam uwagę na zasadę, że różnica między dwiema liczbami pozostaje niezmieniona, jeśli dodamy lub odejmiemy tę samą wartość od obu liczb. W oparciu o tę zasadę możemy stosować sprytne skróty w odejmowaniu.
Przykład: Rozważmy odejmowanie: \(73\ 485 – 68\ 697\). Możemy uprościć to działanie, dodając tę samą wartość do obu liczb tak, aby odjemnik stał się ,,okrągły”:
73 485 - 68 697
+ 3 + 3 (dodajemy 3 do obu liczb)
------------------
73 488 - 68 700
+ 300 + 300 (dodajemy 300 do obu liczb)
------------------
73 788 - 69 000
+ 1000 + 1000 (dodajemy 1000 do obu liczb)
------------------
74 788 - 70 000 = 4 788Te strategie, choć na pierwszy rzut oka mogą wydawać się bardziej skomplikowane, w rzeczywistości promują głębsze zrozumienie relacji między liczbami i rozwijają zdolność do efektywnego rachunku pamięciowego. Klocki Cuisenaire’a stanowią doskonałe narzędzie do wizualizacji tych technik, czyniąc abstrakcyjne strategie intuicyjnymi i praktycznymi.
Klocki Cuisenaire’a sprawiają, że ,,przenoszenie” i ,,rozmienianie” przestają być magicznymi ruchami, a stają się logicznymi i intuicyjnymi manipulacjami długościami, które budują głębokie zrozumienie systemu dziesiętnego.


