Czy matematyka bywa dla Twojego dziecka, a może i dla Ciebie, abstrakcyjnym labiryntem cyfr i symboli? Pamiętasz, jak trudno było zrozumieć, czym właściwie jest \(3 \cdot 5\) albo czym różni się \(\frac{1}{2}\) od \(\frac{2}{4}\)? Na szczęście, Klocki Cuisenaire’a przychodzą z pomocą, oferując konkretne, namacalne narzędzie do wizualizacji podstawowych operacji matematycznych.
W naszym poprzednim cyklu artykułów odkrywaliśmy, jak te kolorowe klocki rozwijają wyobraźnię przestrzenną. Dziś zanurzymy się w ich równie fascynujące zastosowanie w świecie liczb. Klocki Cuisenaire’a to nie tylko pomoc dydaktyczna – to system, który ma swoje ,,zasady gry”. I tak jak w sporcie, gdzie zasady gry są ściśle określone (choć równie dobrze mogłyby być inne), tak i w świecie klocków Cuisenaire’a istnieją ustalone konwencje. Używanie tych ustalonych zasad pozwala nam komunikować się i uczyć efektywniej, budując wspólny język matematyki.
Zatem, przygotujcie swoje klocki! Pokażemy Wam, jak te proste, kolorowe narzędzia pomogą zrozumieć podstawy dodawania, odejmowania, mnożenia, dzielenia i ułamków, torując drogę do myślenia algebraicznego!
Klocki Cuisenaire’a
Zacznijmy od przypomnienia podstawowych oznaczeń klocków, które są fundamentem naszej pracy:
- Biały (BIA): 1 cm
- Czerwony (CZE): 2 cm
- Jasnozielony (JZI): 3 cm
- Fioletowy (FIO): 4 cm
- Żółty (ŻÓŁ): 5 cm
- Ciemnozielony (CZI): 6 cm
- Czarny (CZA): 7 cm
- Brązowy (BRĄ): 8 cm
- Niebieski (NIE): 9 cm
- Pomarańczowy (POM): 10 cm

Dodawanie: budowanie ,,pociągów”
Dodawanie z klockami Cuisenaire’a to nic innego jak budowanie ,,pociągów”. Kładziemy klocki jeden za drugim, koniec do końca, aby stworzyć długą linię. Wynik sumy to pojedynczy klocek, który idealnie pasuje do długości naszego pociągu.
Przykład: \( \text{CZE} + \text{JZI} = \text{ŻÓŁ} \)

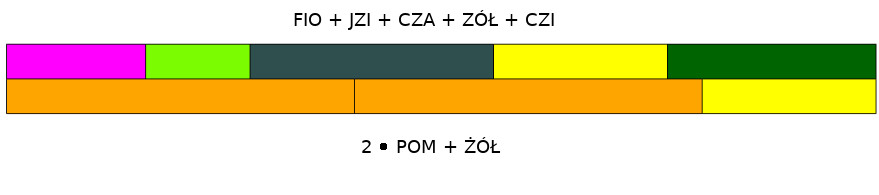
Jeśli pociąg jest dłuższy niż pomarańczowy klocek (\(10\)), używamy kombinacji pomarańczowych klocków i krótszego klocka, który uzupełni długość.
Na przykład, jeśli BIA \( = 1\), to: \[ \text{FIO} + \text{JZI} + \text{CZA} + \text{ŻÓŁ} + \text{CZI} = 25 \]\[4 + 3 + 7 + 5 + 6 = 25\]
Odejmowanie: znajdowanie brakującej części
Odejmowanie z klockami Cuisenaire’a to wizualne poszukiwanie różnicy. Kładziemy mniejszy klocek na większy (lub tuż obok niego) i szukamy klocka, który idealnie wypełni lukę lub wyrówna długości.
Przykład: \( \text{CZI} – \text{FIO} = \text{CZE} \)

Mnożenie: “krzyże” i “wieże”
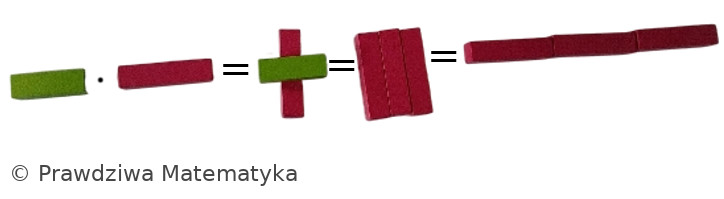
Mnożenie z klockami Cuisenaire’a zyskuje fascynującą, przestrzenną formę. Aby pomnożyć \( \text{FIO} \cdot \text{JZI}\) (czytane jako “fioletowy przez jasnozielony”):
- Układamy klocek
FIO(\(4\)) na spodzie. - Tworzymy ,,krzyż” z klocka
JZI(\(3\)) umieszczonego prostopadle naFIO. - ,,Krzyż” reprezentuje liczbę klocków
FIO, które utworzyłyby ,,podłogę” pod klockiemJZI, tzn. wyobrażamy sobie, ile klockówFIOzmieściłoby się, aby stworzyć prostokąt \(3 \times 4\). - Następnie układamy te klocki
FIOjeden za drugim, tworząc pociąg, aby znaleźć ich łączną wartość. W tym przypadku \(3\) klockiFIOdadzą długość \(12\), czyli \( \text{POM} + \text{CZE} \).
Przykład: \[ \text{JZI} \cdot \text{FIO} = \text{POM} + \text{CZE} \] \[4 \cdot 3 = 12\]
Gdy mnożymy więcej niż dwie wartości, tworzymy ,,wieże” z klocków. Na przykład, ,,krzyż” NIE przez CZI (\( \text{NIE} \cdot \text{CZI} \)) może być z kolei ,,skrzyżowany” z klockiem ŻÓŁ, tworząc wieżę ( \( \text{NIE} \cdot \text{CZI} \cdot \text{ŻÓŁ} \)). Wieże mogą być dowolnej wysokości!
Przykład: \[ \text{NIE} \cdot \text{CZI} \cdot \text{ŻÓŁ} \] \[9\cdot6\cdot5\]

Ułamki: wizualizacja części całości
W artykule dotyczącym relacji już mówiliśmy o nazywaniu klocków w odniesieniu do innych, pokazując ich wzajemne rozmiary. To standardowa metoda prezentowania ułamków za pomocą klocków.
W parze klocków, drugi klocek (mianownik) reprezentuje jednostkę, czyli “całość”. Pierwszy klocek (licznik) jest częścią tej całości.
Przykłady:
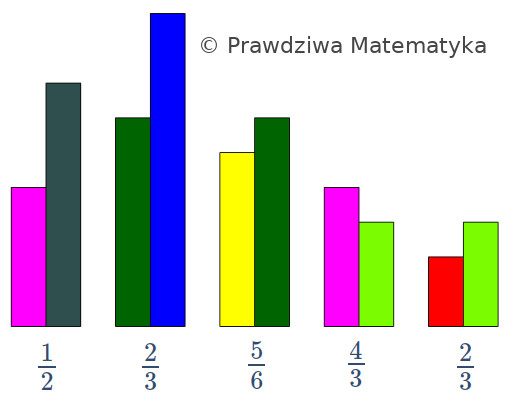
- \(\frac{\text{FIO}}{\text{CZA}} = \frac{1}{2}\) (fioletowy jest połową czarnego)
- \(\frac{\text{CZI}}{\text{NIE}} = \frac{2}{3}\) (ciemnozielony to dwie trzecie niebieskiego)
- \(\frac{\text{ŻÓŁ}}{\text{CZI}}= \frac{5}{6}\) (żółty to pięć szóstych ciemnozielonego)
- \(\frac{\text{FIO}}{\text{JZI}}= \frac{4}{3}\) (fioletowy to cztery trzecie jasnozielonego)
- \(\frac{\text{CZE}}{\text{JZI}}= \frac{2}{3}\) (czerwony to dwie trzecie jasnozielonego)
Mnożenie ułamków odbywa się z ułamkami w tej formie. Czasami w operacjach na ułamkach używa się tylko klocka licznika, a mianownik jest rozumiany jako stała jednostka.

Dzielenie: ile razy coś się zmieści?
Dzielenie może być postrzegane na kilka sposobów z klockami Cuisenaire’a.
Dzielenie jako ułamek
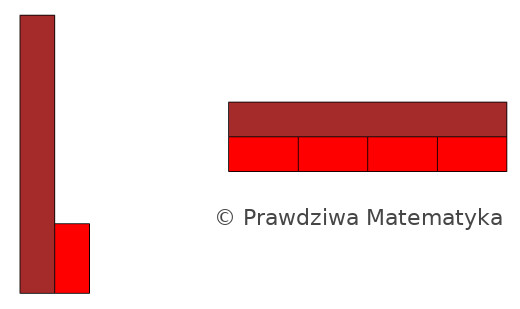
Samo wyrażenie \[ \frac{\text{BRĄ}}{\text{CZE}} = \text{BRĄ} : \text{CZE} \] jest formą pytania “ile razy klocek CZE mieści się w klocku BRĄ?”.
Żeby odpowiedzieć na to pytanie, budujemy odpowiedni ,,pociąg”.
Dzielenie jako wielokrotne odejmowanie (przypadek bez reszty)
Dzielenie \(20\) przez \(4\) to znalezienie odpowiedzi na pytanie: “ile razy mogę wydzielić grupę rozmiaru 4, mając 20 jedności?” \[20 – (x \cdot 4) = 0.\] Aby znaleźć odpowiedź, jeśli \(\text{BIA} = 1\), zbuduj pociąg o długości \(20\) (dwa klocki POM) i spróbuj dopasować do niego pociąg złożony z samych klocków FIO (\(4\)). Liczba klocków FIO w pociągu to wynik dzielenia.
\[20:4=x\]\[20-(x\cdot4)=0\]\[20-(5\cdot4)=0\]\[x=5\]\[20:4=5\]

Dzielenie jako wielokrotne odejmowanie (przypadek z resztą)
Dzielenie \(19\) przez \(4\) to znalezienie odpowiedzi na pytanie: “ile razy mogę wydzielić grupę rozmiaru 4, mając 19 jedności i ile pozostanie?” \[19 – (x \cdot 4) + r = 0.\] Aby znaleźć odpowiedź, jeśli \(\text{BIA} = 1\), zbuduj pociąg o długości \(19\) (klocki POM i NIE) i spróbuj dopasować do niego pociąg złożony z samych klocków FIO (\(4\)), a następnie uzupełnij pociąg pasującym klockiem JZI (\(3\)). Liczba klocków FIO w pociągu to wynik dzielenia, a wartość klocka JZI to reszta.
\[19-(x\cdot4) + r=0\]\[19-(4\cdot4) + 3=0\]\[x=4, r=3\]\[19:4=4 \text{ reszta } 3\]

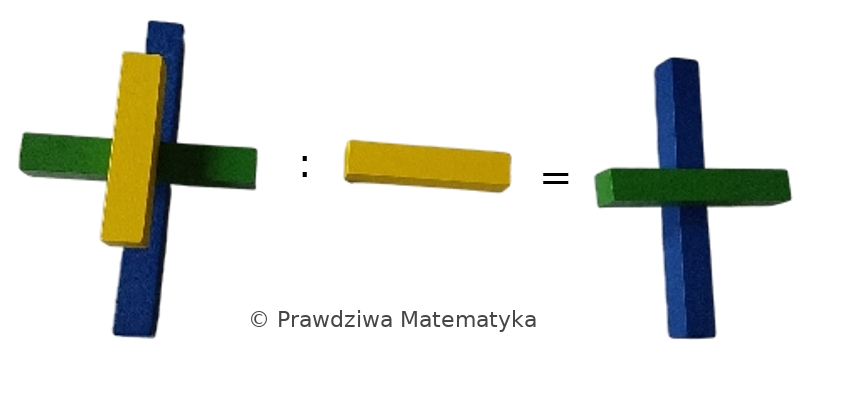
Dzielenie jako operacja odwrotna do mnożenia
Jeżeli mnożenie było zamodelowane za pomocą budowy wieży z klocków, dzielenie można wykonać poprzez usunięcie klocka z wieży.
\[\text{NIE}\cdot\text{CZI}\cdot\text{ŻÓŁ}:\text{ŻÓŁ}=\text{NIE}\cdot\text{CZI}\]
Klocki Cuisenaire’a to nie tylko kolorowe patyczki, ale potężne narzędzie do zrozumienia abstrakcyjnych pojęć matematycznych. Dają konkretne podstawy do budowania intuicji numerycznej, która jest niezbędna zarówno w podstawowej arytmetyce, jak i w bardziej zaawansowanej algebrze. Zacznijcie budować, eksperymentować i odkrywać – matematyka nigdy nie była tak namacalna!


