Kontynuujemy naszą podróż po świecie arytmetyki z Klockami Cuisenaire’a! Po opanowaniu dodawania i odejmowania, nadszedł czas na mnożenie – operację, która bywa dla wielu dzieci (i dorosłych!) bardziej abstrakcyjna. Klocki Cuisenaire’a oferują jednak konkretny sposób na zrozumienie, czym właściwie jest mnożenie i jak działają jego fundamentalne prawa.
Przyjmijmy, że biały klocek (BIA) będzie naszą jednostką (\(1\)). Jest to bardzo ważne, ponieważ użycie innej jednostki w mnożeniu liczb naturalnych może prowadzić do skomplikowanych interpretacji wyników, co może być mylące na początkowym etapie nauki.
Mnożenie: ,,krzyże” i ,,podłogi”
Aby pomnożyć dwa klocki, na przykład klocek FIO (fioletowy) przez klocek JZI (jasnozielony) (\(\text{FIO} \cdot \text{JZI}\)):

Krok I:
Kładziemy klocek FIO (\(4\)).
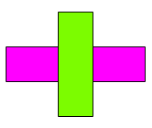
Krok II:
Układamy klocek JZI (\(3\)) na klocku FIO, prostopadle do niego, tworząc ,,krzyż”. Ten ,,krzyż” symbolizuje, że bierzemy tyle klocków FIO, ile mieści się na ,,podłodze” pod klockiem JZI, ułożonych w poprzek.
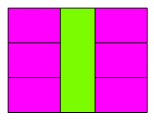
Krok III:
Wyobrażamy sobie, ile klocków FIO byłoby potrzebnych, aby stworzyć prostokątną ,,podłogę” pod klockiem JZI. W tym przypadku będą to trzy klocki FIO.
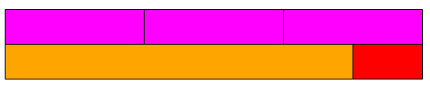
Krok IV:
Następnie układamy te trzy klocki FIO jeden za drugim, tworząc ,,pociąg”, aby znaleźć wynik mnożenia. Trzy klocki FIO dadzą długość \(12\), czyli \( \text{POM} + \text{CZE} \).
Ostatecznie: \[ \text{FIO} \cdot \text{JZI} = \text{POM} + \text{CZE}, \] bo \(4 \cdot 3 = 12\).
Prawo przemienności mnożenia
Mnożenie, podobnie jak dodawanie, jest operacją przemienną. Oznacza to, że kolejność czynników nie wpływa na wynik. Klocki Cuisenaire’a doskonale to demonstrują. Wykonajmy to samo działanie, co wcześniej, ale zamieńmy czynniki kolejnością: (\(\text{JZI} \cdot \text{FIO}\)).

Krok I:
Kładziemy klocek JZI (\(3\)).
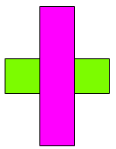
Krok II:
Układamy klocek FIO (\(4\)) na klocku JZI, prostopadle do niego, tworząc ,,krzyż”. Ten ,,krzyż” symbolizuje, że bierzemy tyle klocków JZI, ile mieści się na ,,podłodze” pod klockiem FIO, ułożonych w poprzek.
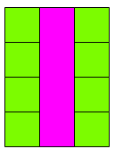
Krok III:
Wyobrażamy sobie, ile klocków JZI byłoby potrzebnych, aby stworzyć prostokątną ,,podłogę” pod klockiem FIO. W tym przypadku będą to cztery klocki JZI.
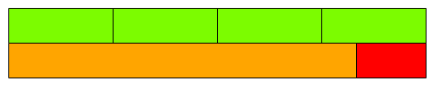
Krok IV:
Następnie układamy te cztery klocki JZI jeden za drugim, tworząc ,,pociąg”, aby znaleźć wynik mnożenia. Cztery klocki JZI dadzą długość \(12\), czyli \( \text{POM} + \text{CZE} \).
Ostatecznie: \[ \text{JZI} \cdot \text{FIO} = \text{POM} + \text{CZE}, \] bo \(3 \cdot 4 = 12\).
Wizualizując oba ,,krzyże”, łatwo zauważyć, że powierzchnia ,,podłogi” jest taka sama, niezależnie od kolejności, w jakiej ułożymy klocki, a zatem widzimy, że kolejność, w jakiej mnożymy liczby nie ma znaczenia.
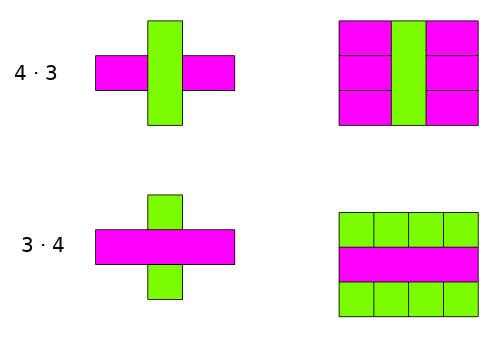
Prawo łączności mnożenia: budowanie ,,wież”
Mnożenie jest operacją dwuargumentową, co oznacza, że jednocześnie możemy pomnożyć tylko dwie liczby. Jednakże, jeśli mamy grupę liczb do pomnożenia, prawo łączności mówi nam, że kolejność grupowania czynników nie ma znaczenia. W świecie Klocków Cuisenaire’a mnożenie trzech lub więcej klocków odbywa się poprzez budowanie ,,wież”.
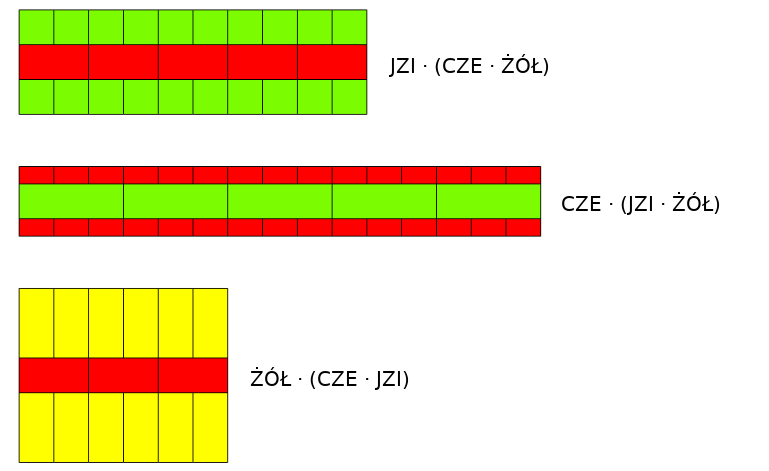
Przykład: \( \text{JZI} \cdot \text{CZE} \cdot \text{ŻÓŁ} \) (czyli \(3 \cdot 2 \cdot 5\)):

Sposób 1: \( \text{JZI} \cdot (\text{CZE} \cdot \text{ŻÓŁ}) \)
Krok I:
Zaczynamy od iloczynu klocków z góry wieży: \[ \text{CZE} \cdot \text{ŻÓŁ},\] co daje w wyniku ,,pociąg” pasujący do klocka POM.

Krok II:
Zastępujemy dwa górne klocki wieży klockiem POM (czyli wynikiem obliczonego przed chwilą iloczynu) i obliczamy iloczyn \[\text{JZI}\cdot\text{POM}.\]

Krok III:
Łatwo zauważyć, że ,,podłoga” utworzona z \(10\) klocków JZI jest tak samo duża, jak ,,podłoga” z \(3\) klocków POM, a zatem przeskakujemy krok budowania ,,pociągu” z klocków JZI i dopasowywania do nich kloców POM, bo z góry wiemy, że wynikiem tego dopasowania będzie ,,pociąg” złożony z \(3\) klocków POM.

Krok IV:
Wynikiem mnożenia \[ \text{JZI} \cdot (\text{CZE} \cdot \text{ŻÓŁ}) \] jest \(3\cdot\text{POM}\).

Możemy to zapisać na liczbach w następujący sposób:
\(3\cdot(2\cdot5)=3\cdot10=30.\)
Sposób 2: \(( \text{JZI} \cdot \text{CZE} ) \cdot \text{ŻÓŁ}\)
Krok I:
Zaczynamy od iloczynu klocków z dołu wieży: \[ \text{JZI} \cdot \text{CZE},\] co daje w wyniku ,,pociąg” pasujący do klocka CZI.

Krok II:
Zastępujemy dwa dolne klocki wieży klockiem CZI (czyli wynikiem obliczonego przed chwilą iloczynu) i obliczamy iloczyn \[\text{CZI}\cdot\text{ŻÓŁ}.\]

Krok III:
Układamy ,,pociąg” z \(5\) klocków CZI, które tworzyły ,,podłogę” pod klockiem ŻÓŁ. Długość tego ,,pociągu” odpowiada ,,pociągowi” utworzonemu z \(3\) klocków POM.

Krok IV:
Wynikiem mnożenia \[ (\text{JZI} \cdot \text{CZE}) \cdot \text{ŻÓŁ} \] jest \(3\cdot\text{POM}\).

Możemy to zapisać na liczbach w następujący sposób:
\((3\cdot2)\cdot5=6\cdot5=30.\)
Oba powyższe sposoby wykonywania obliczeń dały taki sam wynik, co jest przykładem potwierdzającym własność łączności mnożenia:
\[ \text{JZI} \cdot (\text{CZE} \cdot \text{ŻÓŁ}) = (\text{JZI} \cdot \text{CZE}) \cdot \text{ŻÓŁ}.\]
Stosując jednocześnie prawo łączności i prawo przemienności mnożenia, łatwo można pokazać, że ten sam wynik uzyskamy, grupując i przestawiając czynniki w dowolny sposób, na przykład: \( \text{CZE} \cdot (\text{JZI} \cdot \text{ŻÓŁ}) \) lub \( \text{ŻÓŁ} \cdot (\text{CZE} \cdot \text{JZI}) \).
Prawo rozdzielności mnożenia względem dodawania
Prawo rozdzielności jest fundamentem wielu algorytmów mnożenia, w tym mnożenia pisemnego. Klocki Cuisenaire’a pozwalają na jego ,,namacalną” demonstrację.
Przykład: \[ (\text{ŻÓŁ} + \text{CZE}) \cdot \text{JZI} = (\text{ŻÓŁ} \cdot \text{JZI}) + (\text{CZE} \cdot \text{JZI})\]
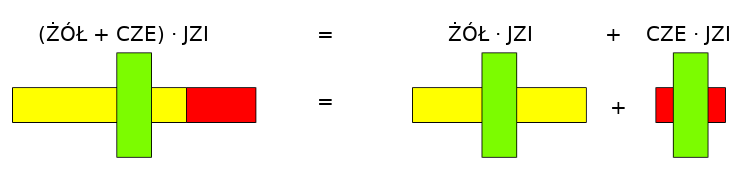
Lewa strona równości:
Obliczamy sumę \( \text{ŻÓŁ} + \text{CZE} = \text{CZA}\)
(tj. \(5 + 2 = 7\)).

Obliczamy iloczyn \(\text{CZA}\cdot\text{JZI}\)
(tj. \(7\cdot3\)) .
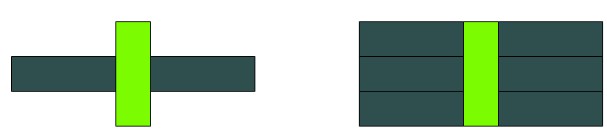
Wynikiem tego iloczynu jest \(2\cdot\text{POM}+\text{BIA}\)
(tj. \(21\)).

Prawa strona równości:
Obliczamy iloczyn \(\text{ŻÓŁ}\cdot\text{JZI}\)
(tj. \(5\cdot3\)).
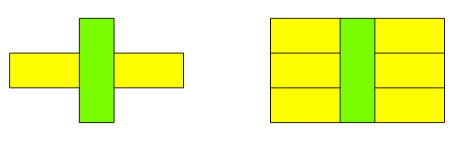
Wynikiem tego iloczynu jest \(\text{POM}+\text{ŻÓŁ}\)
(tj. \(15\)).

Obliczamy iloczyn \(\text{CZE}\cdot\text{JZI}\)
(tj. \(2\cdot3\)).

Wynikiem tego iloczynu jest \(\text{CZI}\)
(tj. \(6\)).

Porównujemy wartości otrzymane po lewej i po prawej stronie równości:

\(2\cdot\text{POM}+\text{BIA} = (\text{POM}+\text{ŻÓŁ})+\text{CZI}\)
(tj. \(21=15+6\)).
Widzimy, że obie strony równania dają ten sam wynik, co wizualnie potwierdza prawo rozdzielności mnożenia względem dodawania.
Prawo rozdzielności mnożenia względem odejmowania
Analogiczne prawo rozdzielności zachodzi także dla odejmowania.
Przykład: \[ (\text{NIE} – \text{FIO}) \cdot \text{JZI} = (\text{NIE} \cdot \text{JZI}) – (\text{FIO} \cdot \text{JZI}) \]
Zacznijmy od obliczenia różnicy po lewej stronie równości: \(\text{NIE} – \text{FIO} = \text{ŻÓŁ}\).
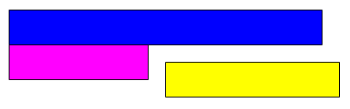
Zatem po lewej stronie równości znajduje się iloczyn \(\text{ŻÓŁ}\cdot\text{JZI}\):
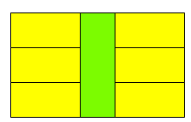
Po prawej stronie znajduje się różnica dwóch iloczynów: \(\text{NIE} \cdot \text{JZI}\) oraz \(\text{FIO} \cdot \text{JZI}\):

Moglibyśmy obliczyć wartość obu iloczynów, a następnie obliczyć ich różnicę, ale dzięki klockom Cuisenaire’a możliwe jest zwizualizowanie wyniku odejmowania z pominięciem żmudnych przekształceń. Odejmowanie przedstawiamy poprzez ułożenie klocków FIO na klockach NIE i w ten sposób widzimy, że szukaną różnicą są \(3\) klocki ŻÓŁ (bo te klocki dopełniłyby klocki FIO do klocków NIE).
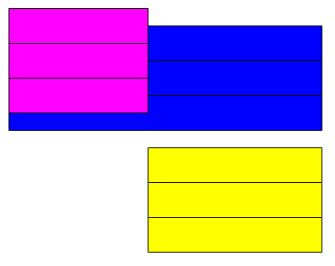
Zarówno po lewej, jak i po prawej stronie otrzymaliśmy tyle samo: \(3\cdot\text{ŻÓŁ}\), a zatem przekonaliśmy się w sposób wizualny o prawie rozdzielności mnożenia względem odejmowania.
Prawa rozdzielności, a tabliczka mnożenia
Znajomość praw rozdzielności jest niezwykle pomocna, zwłaszcza gdy ktoś nie zna całej tabliczki mnożenia. Obliczanie ,,nowego” iloczynu można rozłożyć na prostsze części, opierając się na tym, co uczeń już wie.
Przykład: \(8\cdot9\)
- \(8 \cdot 9 = (8 \cdot 10) – (8 \cdot 1) = 80 – 8 = 72\)
- \(8 \cdot 9 = (5 \cdot 9) + (3 \cdot 9) = 45 + 27 = 72\)
Przykład: \(7\cdot8\)
- \(7\cdot8=(5 \cdot 8)+(2\cdot8)=40+16=56\)
- \(7\cdot8=(7\cdot10) – (7\cdot2)=70-14=56\)
To właśnie elastyczne myślenie o liczbach, które Klocki Cuisenaire’a pomagają rozwijać!
Mnożenie liczb wielocyfrowych
Choć praca z wielocyfrowymi czynnikami za pomocą klocków staje się skomplikowana w praktyce (wymagałaby budowania bardzo dużych ,,wież” i struktur), zrozumienie, że tradycyjny algorytm mnożenia opiera się na podstawowych zasadach rozdzielności, jest kluczowe. Klocki pomagają ugruntować te zasady w konkretny sposób, zanim przejdziemy do abstrakcyjnych symboli.
Tradycyjny algorytm mnożenia (tzw. mnożenie pod kreską) opiera się na prawie rozdzielności. Na przykład, aby pomnożyć \(356 \cdot 27\), musimy wykonać następujące kroki:
- Obliczyć \(356 \cdot 7\) (mnożenie przez jedności).
- Obliczyć \(356 \cdot 20\) (mnożenie przez dziesiątki).
- Zsumować otrzymane wcześniej iloczyny częściowe.
Obliczenie iloczynów częściowych również opiera się na rozdzielności: \[ 356 \cdot 7 = (6 \cdot 7) + (50 \cdot 7) + (300 \cdot 7).\]
Więcej o obliczaniu iloczynu liczb wielocyfrowych w następnym artykule 🙂


