W poprzednim artykule zgłębialiśmy podstawowe zasady mnożenia i jego kluczowe własności, takie jak przemienność, łączność i rozdzielność. Dziś kontynuujemy naszą podróż, skupiając się na praktycznym zastosowaniu prawa rozdzielności w mnożeniu liczb dwucyfrowych – to właśnie tam metoda iloczynów częściowych staje się niezwykle pomocna. Klocki Cuisenaire’a, choć w bardziej zaawansowanych obliczeniach służą głównie do wizualizacji procesu, a nie wykonywania skomplikowanych działań, są niezastąpione w budowaniu intuicyjnego zrozumienia tych mechanizmów.
Wprowadzenie do mnożenia liczb dwucyfrowych
Mnożenie liczb dwucyfrowych na pierwszy rzut oka może wydawać się skomplikowane, ale w rzeczywistości opiera się na prostym i znajomym nam już prawie rozdzielności. Możemy to zademonstrować, przekształcając znane działanie, np. \(8 \cdot 7\), w bardziej rozbudowaną wersję, na przykład:\[ 8\cdot7=(6 + 2) \cdot (4 + 3).\]
Jeśli przyjmiemy biały klocek (BIA) za \(1\), możemy pokazać powyższą równość za pomocą klocków:\[\text{BRĄ}\cdot\text{CZA}=(\text{CZI}+\text{CZE})\cdot(\text{FIO}+\text{JZI}).\]
Przekonamy się, że prostokąt utworzony przez mnożenie klocka BRĄ (\(8\)) przez klocek CZA (\(7\)) jest równy sumie czterech mniejszych prostokątów:
\[ \text{BRĄ}\cdot\text{CZA}=(\text{CZI} \cdot \text{FIO}) + (\text{CZE} \cdot \text{FIO}) + (\text{CZI} \cdot \text{JZI}) + (\text{CZE} \cdot \text{JZI}).\]
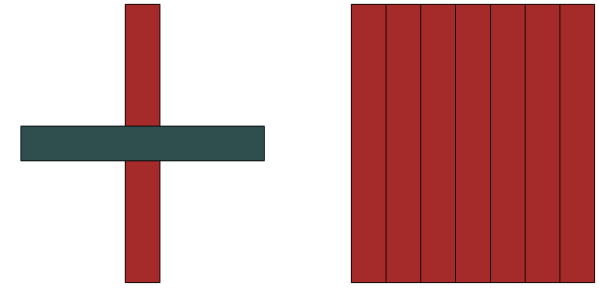
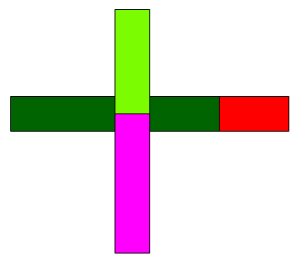
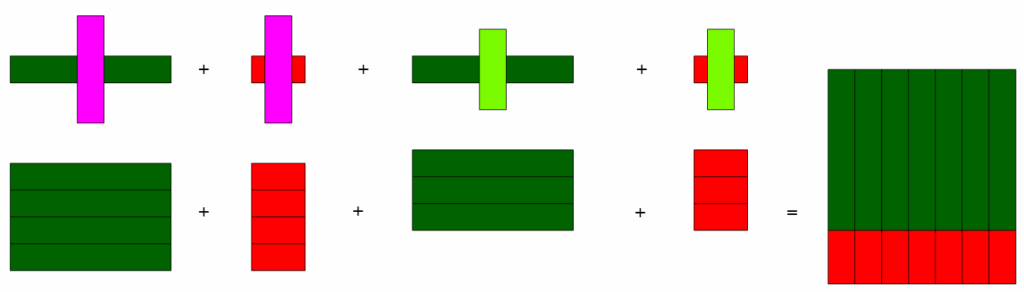
Czyli: \[8\cdot7=(6 + 2) \cdot (4 + 3)\]\[= (6 \cdot 4) + (2 \cdot 4) + (6 \cdot 3) + (2 \cdot 3)\]\[ = 24 + 8 + 18 + 6 = 56 .\]
Ta wizualizacja, choć wymaga sporej wyobraźni przestrzennej przy układaniu klocków, doskonale ugruntowuje przekonanie, że rozłożenie mnożenia na części daje prawidłowy wynik. To nie tylko uczy i wzmacnia fakty dotyczące mnożenia, ale także przekonuje ucznia o słuszności metody.
Mnożenie liczb dwucyfrowych: metoda iloczynów częściowych
Aby pomnożyć, na przykład, \(63\) przez \(25\), rozbijamy obie liczby na dziesiątki i jedności: \( (60 + 3) \cdot (20 + 5) \). Następnie znajdujemy sumę iloczynów częściowych, korzystając z rozszerzonego prawa rozdzielności: \[ (a + b) \cdot (c + d) = (a \cdot c) + (a \cdot d) + (b \cdot c) + (b \cdot d).\]
Liczbę \(60\) oraz \(20\) układamy za pomocą klocków wyrażając je jako iloczyn odpowiednio liczby \(6\) i \(2\) przez \(10\).

Nasze działanie można ułożyć za pomocą klocków w następujący sposób:
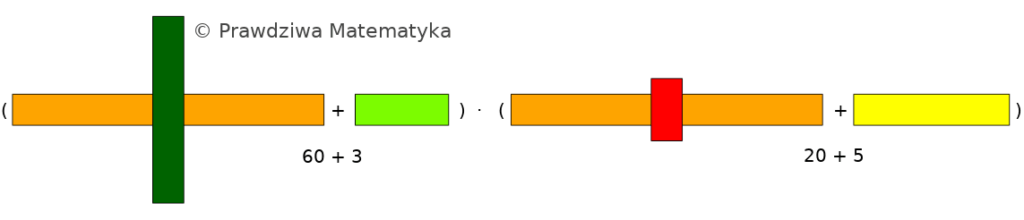
Dla naszego przykładu, rozszerzone prawo rozdzielności mnożenia względem dodawania przyjmuje nastepującą postać: \[ (60 + 3) \cdot (20 + 5) = (60 \cdot 20) + (60 \cdot 5) + (3 \cdot 20) + (3 \cdot 5) .\]
Obliczamy iloczyny częściowe:
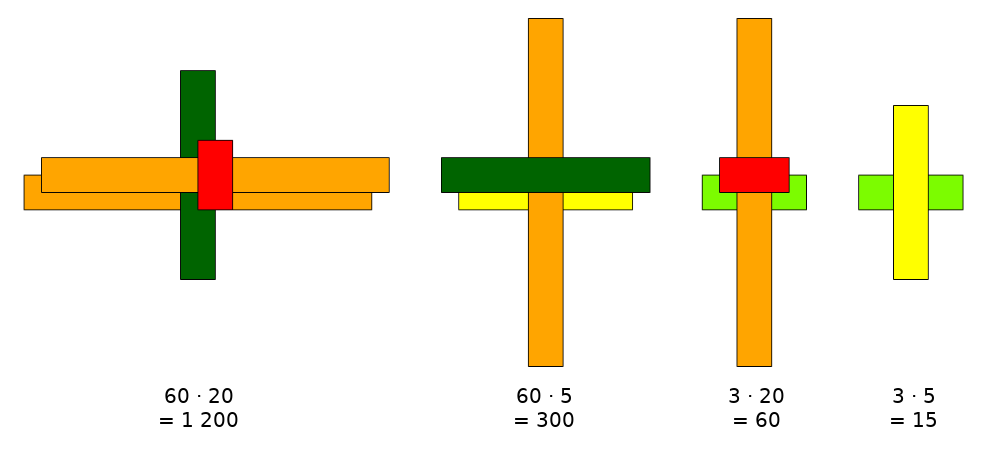
Następnie sumujemy wszystkie iloczyny częściowe: \[15 + 300 + 60 + 1\ 200 = 1\ 575.\]
Tradycyjny algorytm mnożenia pisemnego jest skondensowaną formą zapisu powyższej procedury. W początkowej fazie nauki algorytmu, możemy zapisać każdy iloczyn częściowy oddzielnie:
63
⋅ 25
-----
15 (5 ⋅ 3)
300 (5 ⋅ 60)
60 (20 ⋅ 3)
1200 (20 ⋅ 60)
-----
1575
Dopiero kiedy dziecko dobrze rozumie, skąd się bierze każdy iloczyn częściowy, możemy ograniczyć się do dwóch iloczynów częściowych, zapisując kroki w bardziej skondensowanej formie:
63
⋅ 25
-----
315 (63 ⋅ 5)
1260 (63 ⋅ 20)
-----
1575
Pamiętajmy, że klocki Cuisenaire’a są przede wszystkim narzędziem do wyjaśniania procesu, a nie do wykonywania skomplikowanych obliczeń, gdy sam proces został już zrozumiany. Ich prawdziwa wartość leży w budowaniu intuicji i wizualnego zrozumienia zasad matematycznych, które leżą u podstaw operacji na liczbach.


