W poprzednim artykule odkrywaliśmy liczby parzyste, nieparzyste, pierwsze i złożone za pomocą Klocków Cuisenaire’a. Dziś zanurzymy się głębiej w świat liczb, badając dzielniki oraz fascynujące pojęcie rozkładu na czynniki pierwsze. Klocki pozwolą nam wizualizować te abstrakcyjne idee, budując solidne podstawy dla dalszej nauki matematyki.
Przyjmijmy, że biały klocek \(\text{BIA} = 1\).
Dzielniki liczby
Każdą liczbę można przedstawić jako pociąg z białych klocków. Jeśli biały klocek jest jedynym klockiem, z którego da się utworzyć jednokolorowy pociąg reprezentujący daną liczbę, oznacza to, że ta liczba jest liczbą pierwszą i nie ma innych dzielników poza \(1\) i sobą samą.
Jeśli jednak daną liczbę można przedstawić za pomocą jednokolorowych pociągów złożonych z klocków innych niż białe, to klocki te reprezentują liczby, które są dzielnikami tej liczby.
Przykład: Dzielniki liczby \(24\) Jakie jednokolorowe pociągi mogą osiągnąć długość \(24\)?
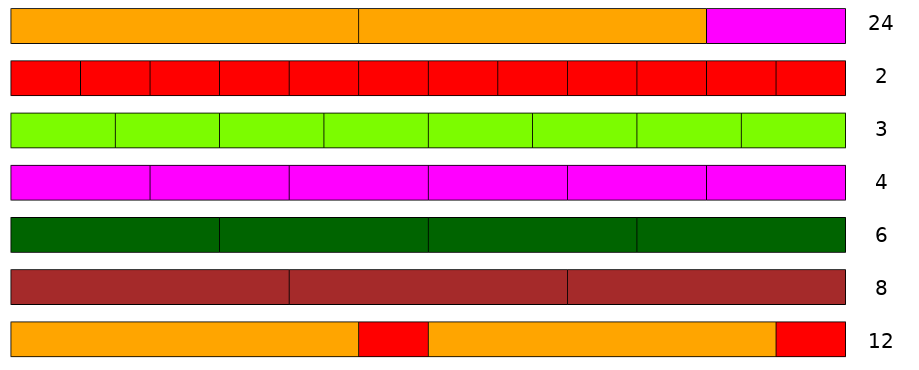
Na podstawie powyższych układów klocków widzimy, że dzielnikami liczby \(24\) (poza \(1\)) są liczby: \(2, 3, 4, 6, 8, 12\).
Wskazówka: W pracy z dzielnikami często przydatne jest stworzenie ,,klocka” o długości \(12\), łącząc klocek POM (\(10\)) i klocek CZE (\(2\)). Możemy go nazwać roboczo ,,pomczerwonym” i oznaczyć jako PCZ. Klocki można skleić ze sobą za pomocą taśmy, ,,plasteliny” do wieszania obrazków na ścianach lub po prostu umówić się, że te dwa klocki ułożone w ,,pociąg” będziemy traktowali jak jeden klocek.
Rozkład na czynniki pierwsze: budowanie ,,wież”
Wszystkie liczby złożone (czyli te, które są większe od \(1\) i nie są pierwsze) mogą być reprezentowane przez wieże zbudowane z ich dzielników.
Przykład: Wieże dla \(24\)
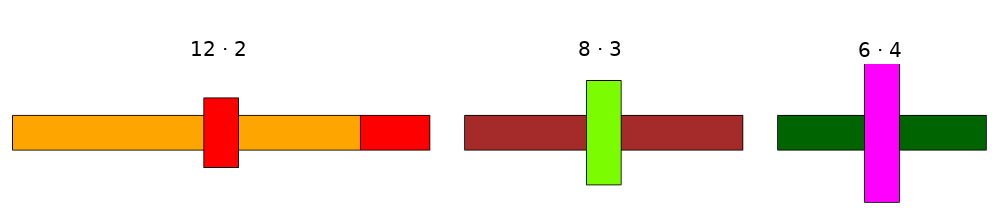
Cztery z dzielników liczby \(24\) (dokładniej: \(4, 6, 8, 12\)) same są liczbami złożonymi i mogą być również rozłożone na wieże zbudowane z liczb pierwszych.
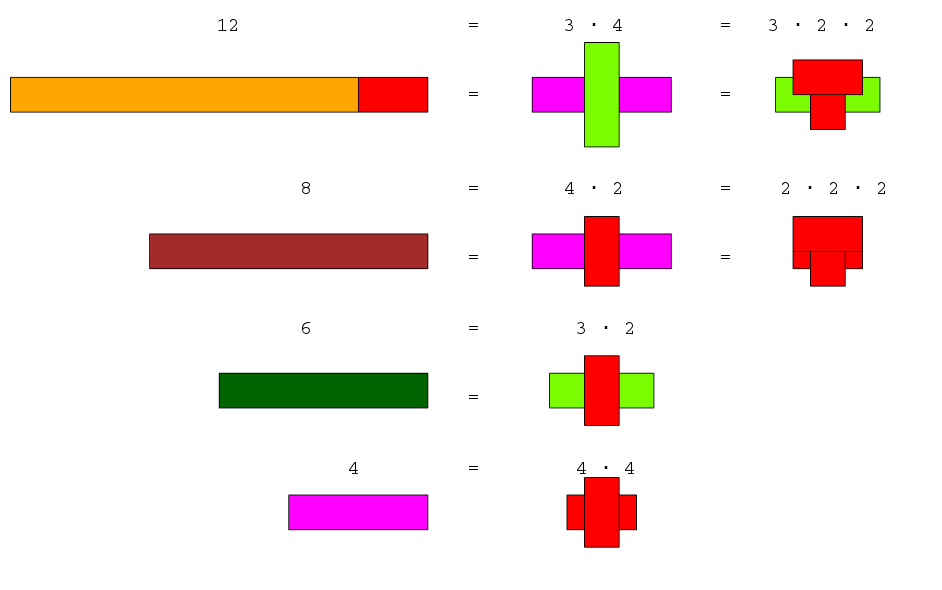
Kluczową ideą jest rozłożenie liczby złożonej na jej czynniki pierwsze, czyli klocki, które reprezentują tylko liczby pierwsze (CZE, JZI, ŻÓŁ, CZA, NIE…). Wieża czynników pierwszych dla \(24\) będzie składać się wyłącznie z czerwonych i jasnozielonych klocków (bo \(2\) i \(3\) są liczbami pierwszymi, a \(24 = 2 \cdot 2 \cdot 2 \cdot 3\)).
Ile klocków CZE i ile klocków JZI jest potrzebnych, aby zbudować wieżę czynników pierwszych dla liczby \(24\)?

Okazuje się, że są to trzy klocki CZE i jeden klocek JZI.
Uwaga: Ważne jest to, że niezależnie od tego, od których czynników zaczniemy rozkładanie liczby złożonej, zawsze skończymy z tymi samymi ,,cegiełkami” w naszej wieży czynników pierwszych. Zmieni się tylko kolejność, w jakiej je ułożymy.
Przykład: Czynniki pierwsze dla \(36\)
Możemy stworzyć wiele wież dla liczby \(36\):
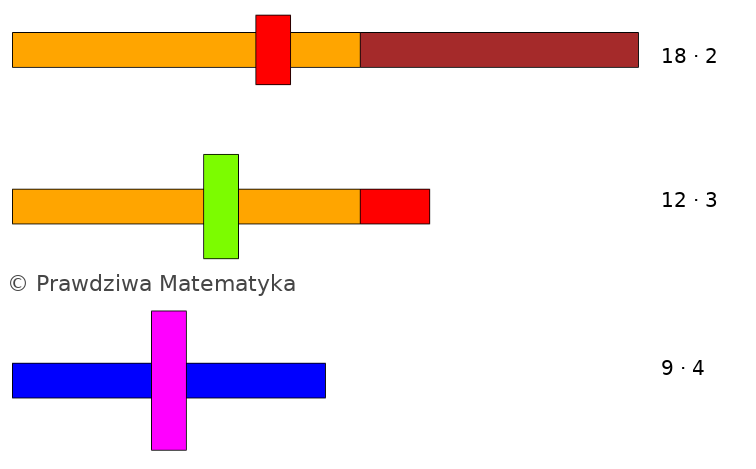
Ale jeśli naszym celem jest budowanie wież wyłącznie z klocków reprezentujących liczby pierwsze, należy każdą z liczb złożonych zastąpić odpowiednią ,,wieżą”:
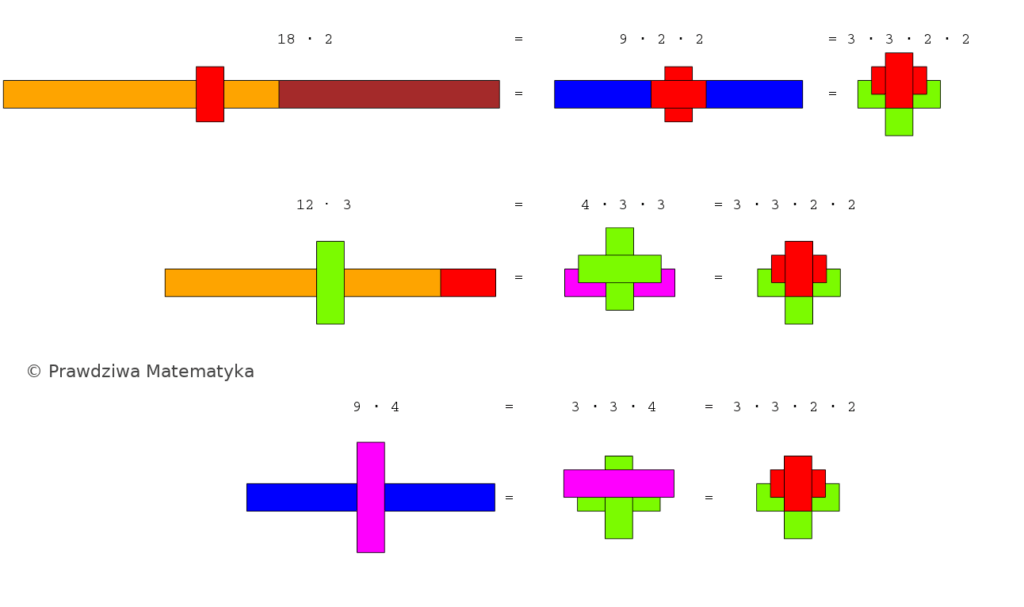
Tak więc, niezależnie od tego, od której wieży dla \(36\) zaczniemy, ostatecznie otrzymamy te same ,,cegiełki” pierwszych czynników: dwa klocki CZE (\(2\)) i dwa klocki JZI (\(3\)), co daje \[2 \cdot 2 \cdot 3 \cdot 3 = 36.\]
Wspólne dzielniki i Największy Wspólny Dzielnik (NWD)
Czerwony klocek (CZE) jest dzielnikiem zarówno fioletowego klocka (FIO), jak i pomarańczowego klocka (POM). Nazywamy go wspólnym dzielnikiem tych dwóch liczb. Aby znaleźć wspólne dzielniki dwóch liczb, budujemy ich wieże złożone z czynników pierwszych i sprawdzamy, jakie klocki (czynniki pierwsze) znajdują się w obu wieżach.
Przykład: Wspólne czynniki liczb \(42, 56\) i \(98\)
Rozkładamy wszystkie liczby na iloczyn czynników pierwszych:
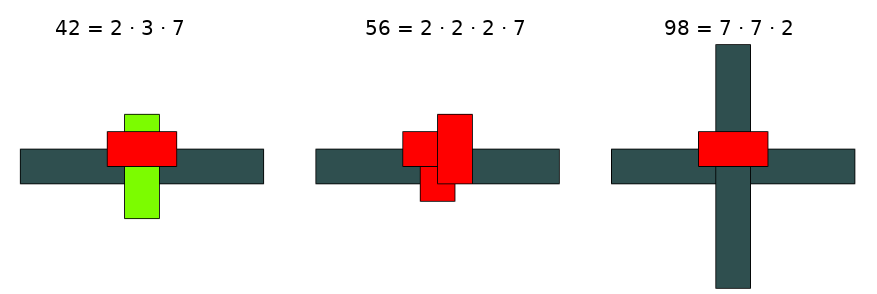
Wspólne klocki (czynniki pierwsze) we wszystkich trzech wieżach to:
- Jeden klocek CZE (\(2\))
- Jeden klocek CZA (\(7\))
Zatem wspólne czynniki liczb \(42, 56\) i \(98\) to \(2, 7\) oraz ich iloczyn: \(2 \cdot 7 = 14\).

Największy Wspólny Dzielnik (NWD) to \(14\), który jest zawsze iloczynem wszystkich wspólnych czynników pierwszych.
Jak widać na poniższej grafice, każdą z liczb \(42, 56\) oraz \(98\) można ułożyć z klocków jako iloczyn liczby \(14\) przez jakąś liczbę naturalną. Wnioskujemy z tego, że każda z tych liczb jest wielokrotnością liczby \(14\), a zatem liczba \(14\) jest jednocześnie dzielnikiem każdej z nich. Jest to największy wspólny dzielnik, bo żaden inny klocek (ani układ klocków) nie powtarza się we wszystkich ,,wieżach”.
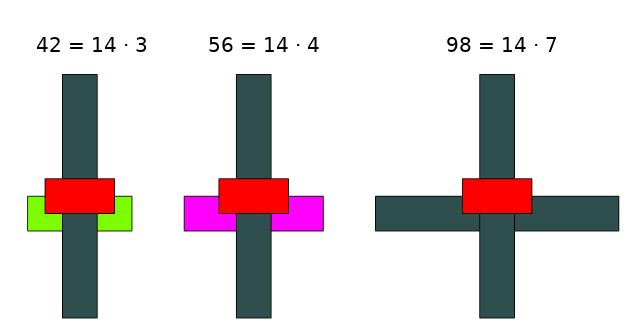
Znajdowanie wszystkich dzielników liczby
Kiedy już zbudujemy wieżę czynników pierwszych dla danej liczby, możemy z łatwością znaleźć wszystkie jej dzielniki, grupując ,,cegiełki” tej wieży na wszystkie możliwe sposoby.
Przykład: Dzielniki liczby \(420\)
Wieża czynników pierwszych dla \(420\) to: \(2 \cdot 2 \cdot 3 \cdot 5 \cdot 7\), co pokazujemy za pomocą klocków jako iloczyn CZE \(\cdot\) CZE \(\cdot\) JZI \(\cdot\) ŻÓŁ \(\cdot\) CZA.

Możemy teraz grupować te klocki na różne sposoby, aby znaleźć wszystkie czynniki:
- Pojedyncze klocki (czynniki pierwsze):
- \(2, 3, 5, 7\)
- Grupy dwóch klocków:
- \(2 \cdot 2 = 4\),
- \(2 \cdot 3 = 6\),
- \(2 \cdot 5 = 10\),
- \(2 \cdot 7 = 14\),
- \(3 \cdot 5 = 15\),
- \(3 \cdot 7 = 21\),
- \(5 \cdot 7 = 35\)
- Grupy trzech klocków:
- \(2 \cdot 2 \cdot 3 = 12\),
- \(2 \cdot 2 \cdot 5 = 20\),
- \(2 \cdot 2 \cdot 7 = 28\),
- \(2 \cdot 3 \cdot 5 = 30\),
- \(2 \cdot 3 \cdot 7 = 42\),
- \(2 \cdot 5 \cdot 7 = 70\),
- \(3 \cdot 5 \cdot 7 = 105\)
- Grupy czterech klocków:
- \(2 \cdot 2 \cdot 3 \cdot 5 = 60\),
- \(2 \cdot 2 \cdot 3 \cdot 7 = 84\),
- \(2 \cdot 2 \cdot 5 \cdot 7 = 140\),
- \(2 \cdot 3 \cdot 5 \cdot 7 = 210\)
- Grupa pięciu klocków (sama liczba):
- \(2 \cdot 2 \cdot 3 \cdot 5 \cdot 7 = 420\)
Dodatkowo zawsze mamy czynnik \(1\). Zatem wszystkimi dzielnikami liczby \(420\) są: \[1, 2, 3, 4, 5, 6,\]\[7, 10, 12, 14, 15, 20,\]\[ 21, 28, 30, 35, 42, 60,\]\[ 70, 84, 105, 140, 210, 420.\]


