W świecie nauki matematyki, gdzie abstrakcja często bywa wyzwaniem, Klocki Cuisenaire’a jawią się jako oaza konkretu i intuicji. Ale zanim zagłębimy się w szczegółowe lekcje i zaawansowane zastosowania, warto poświęcić czas na… zabawę. Pierwsze spotkanie z tymi kolorowymi klockami powinno być niczym nieskrępowaną, radosną eksploracją 🙂
Zapomnijcie na chwilę o podręcznikach, szczegółowych planach lekcji czy gotowych scenariuszach. Prawdziwym przewodnikiem w przypadku Klocków Cuisenaire’a jest samo pudełko z klockami. Dajcie im swobodę, a same dostarczą bogactwo instrukcji i inspiracji. Nasza rola polega jedynie na stworzeniu przestrzeni do eksperymentowania i delikatnym naprowadzaniu.
Klocki Cuisenaire’a to narzędzie – podobnie jak kreda, cyrkiel czy papier milimetrowy. Ich siła tkwi w uniwersalności i możliwości adaptacji do każdego poziomu nauczania, dowolnego podręcznika i programu nauczania. Nie są one przeznaczone dla konkretnych klas, ale dla konkretnych pojęć matematycznych – od mnożenia, przez liczby pierwsze, aż po wykonywanie pomiarów.
Mniej znaczy więcej
W przeciwieństwie do tradycyjnych podejść, szczegółowe plany lekcji i gotowe karty pracy mogą paradoksalnie ograniczać kreatywność. Dlatego kluczem jest pozwolenie dzieciom na swobodną zabawę z klockami i dostarczanie im jak najmniej informacji wstępnych. To właśnie w tej swobodnej eksploracji rodzi się prawdziwe zrozumienie.
Pierwsze 20 minut z klockami
Jeśli to Twoje pierwsze spotkanie z Klockami Cuisenaire’a, wysyp cały zestaw na stół i baw się nimi przez co najmniej 20 minut, w dowolny sposób, jaki przyjdzie Ci do głowy. Nie czytaj dalszej części tego tekstu – po prostu oddaj się zabawie!
To samo dotyczy Twoich uczniów. Niezależnie od poziomu, na którym uczysz, pozwól im zacząć w ten sam sposób.
Fundament: budowanie schodów
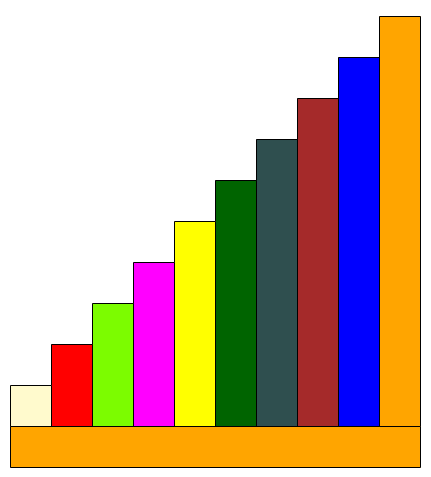
Po swobodnej zabawie, która pozwoli na oswojenie się z klockami, warto wprowadzić konstrukcję schodów. To fundamentalne ćwiczenie, które pozwala zrozumieć relacje między klockami. Schody najlepiej ułożyć na płasko, używając dodatkowego pomarańczowego klocka jako podstawy (podłogi). Zapewni to prostą bazę i równomierne rozmieszczenie klocków.
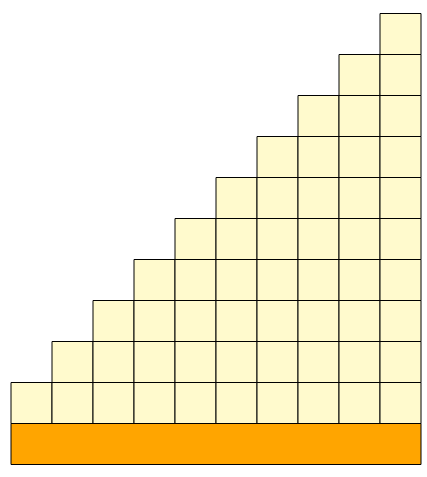
Porównując te schody z takimi, które zostałyby zbudowane wyłącznie z białych klocków, staje się oczywiste, ile białych klocków odpowiada długości każdego kolorowego klocka.
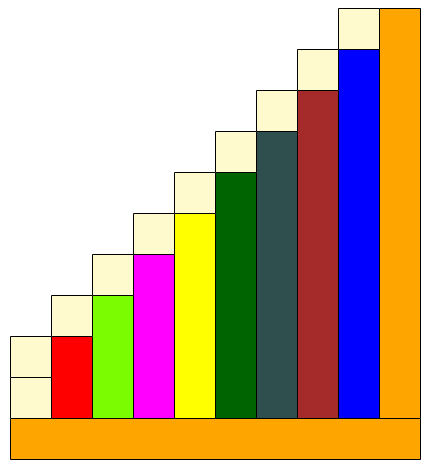
Widać również, że każdy stopień schodów zwiększa się o jeden biały klocek. Można to dodatkowo wzmocnić, kładąc biały klocek na każdym stopniu, aby pokazać, jak pasuje do następnego wyższego stopnia.
Utrwalenie znajomości klocków
Aby efektywnie korzystać z Klocków Cuisenaire’a w nauce matematyki, kluczowe jest płynne rozpoznawanie klocków i ich wzajemnych relacji. Jeśli użytkownik nadal musi mierzyć każdy klocek białymi klockami, aby znaleźć jego względną długość, praca stanie się zbyt żmudna. Dlatego warto poświęcić czas na różnorodne ćwiczenia, które pozwolą na intuicyjne poznanie klocków.
Do nazywania klocków, będziemy posługiwać się skrótami od pierwszych liter ich kolorów:
- Biały (1 cm): BIA
- Czerwony (2 cm): CZE
- Jasnozielony (3 cm): JZI
- Fioletowy (4 cm): FIO
- Żółty (5 cm): ŻÓŁ
- Ciemnozielony (6 cm): CZI
- Czarny (7 cm): CZA
- Brązowy (8 cm): BRĄ
- Niebieski (9 cm): NIE
- Pomarańczowy (10 cm): POM

Zabawy utrwalające znajomość klocków
Oto kilka propozycji zabaw, które pomogą w utrwaleniu znajomości klocków:
Zamknij oczy i spróbuj zobaczyć w wyobraźni kolory klocków tworzących schody.
Z zamkniętymi oczami wybierz największy i najmniejszy z trzech losowo wybranych klocków i zgadnij kolor każdego z nich.
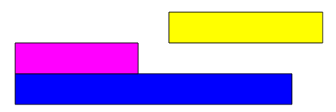
Weź dowolny długi klocek i jeden krótszy od niego. Zgadnij, który klocek należy dołożyć do krótszego, aby uzyskać długość dłuższego klocka.
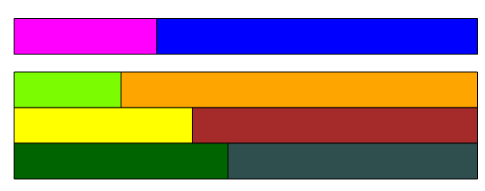
Weź dowolne dwa klocki i połącz je ze sobą, tworząc „pociąg”. Znajdź jak najwięcej innych par klocków, które tworzą pociąg tej samej długości.
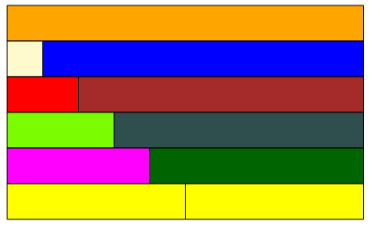
Zbuduj wszystkie dwuklockowe „pociągi” o długości pomarańczowego klocka. Następnie odsuń jeden z każdego pary. Czy potrafisz, patrząc na puste miejsce, odgadnąć, który klocek tam pasuje?
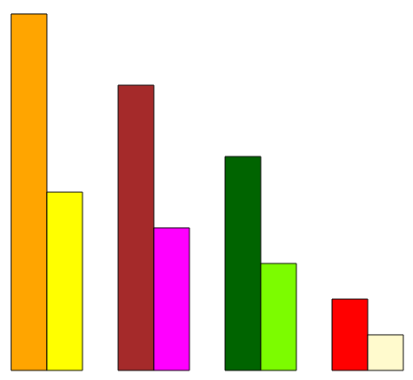
Pomarańczowy klocek jest dwa razy dłuższy od żółtego. Żółty klocek to \(1\over2\) pomarańczowego. Jakie istnieją inne pary tego typu?
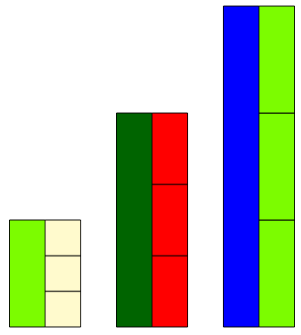
Ciemnozielony klocek jest trzy razy dłuższy od czerwonego; czerwony klocek to \(1\over 3\) ciemnozielonego. Jakie istnieją inne pary tego typu?
Które klocki są 4 razy dłuższe od innego, wybranego klocka? A 5 razy?
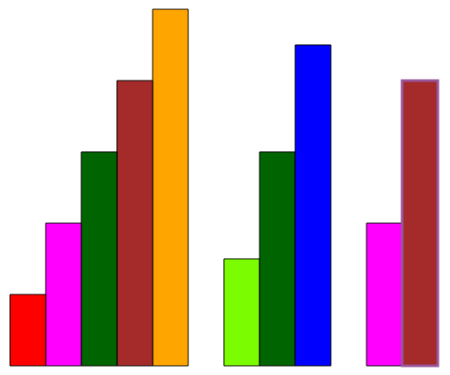
Zbuduj schody, w których stopnie mają wysokość:
- jednego czerwonego klocka
- jednego zielonego klocka
- jednego fioletowego klocka
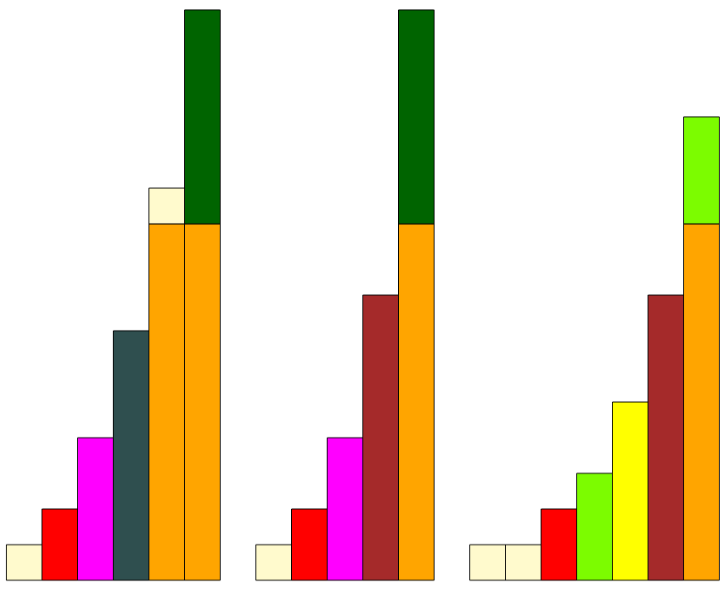
Zbuduj schody, w których wysokość stopni jest nierówna, ale zmienia się w sposób regularny:
- różnica wysokości stopni wzrasta o 1
- różnice wysokości stopni to kolejne potęgi liczby 2
- wysokości schodków tworzą ciąg Fibonacciego
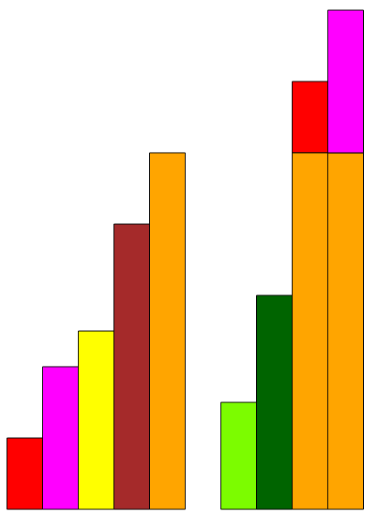
Rozważ schody, w których popełniono błędy:
- Jeden klocek został źle wybrany, który? Co powinno być na jego miejscu?
- Jednego klocka brakuje, którego?
Pamiętajcie, że Klocki Cuisenaire’a to narzędzie, które wspiera odkrywanie matematyki, dlatego pozwólmy dzieciom na eksperymentowanie i swobodną zabawę – to najlepsza droga do głębokiego zrozumienia i pokochania matematyki!


