Czy Twoje dziecko uczy się w klasie 5 i zaczyna mieć trudności z tematami takimi jak Największy Wspólny Dzielnik (NWD) lub Najmniejsza Wspólna Wielokrotność (NWW)? Czy gubi się w gąszczu cech podzielności? Ten moduł to solidna, wizualna i praktyczna podstawa do zrozumienia fundamentów teorii liczb, kluczowych na tym etapie edukacji.
Co Twoje dziecko osiągnie w tym module?
Ten moduł to 15 kompleksowych lekcji, które zapewniają pełne opanowanie następujących zagadnień:
- Parzystość i nieparzystość sum i iloczynów: Dziecko zrozumie, dlaczego m.in. ,,parzysta + parzysta = parzysta”, bo zamodeluje te i podobne własności w sposób wizualny, zamiast uczyć się ich na pamięć.
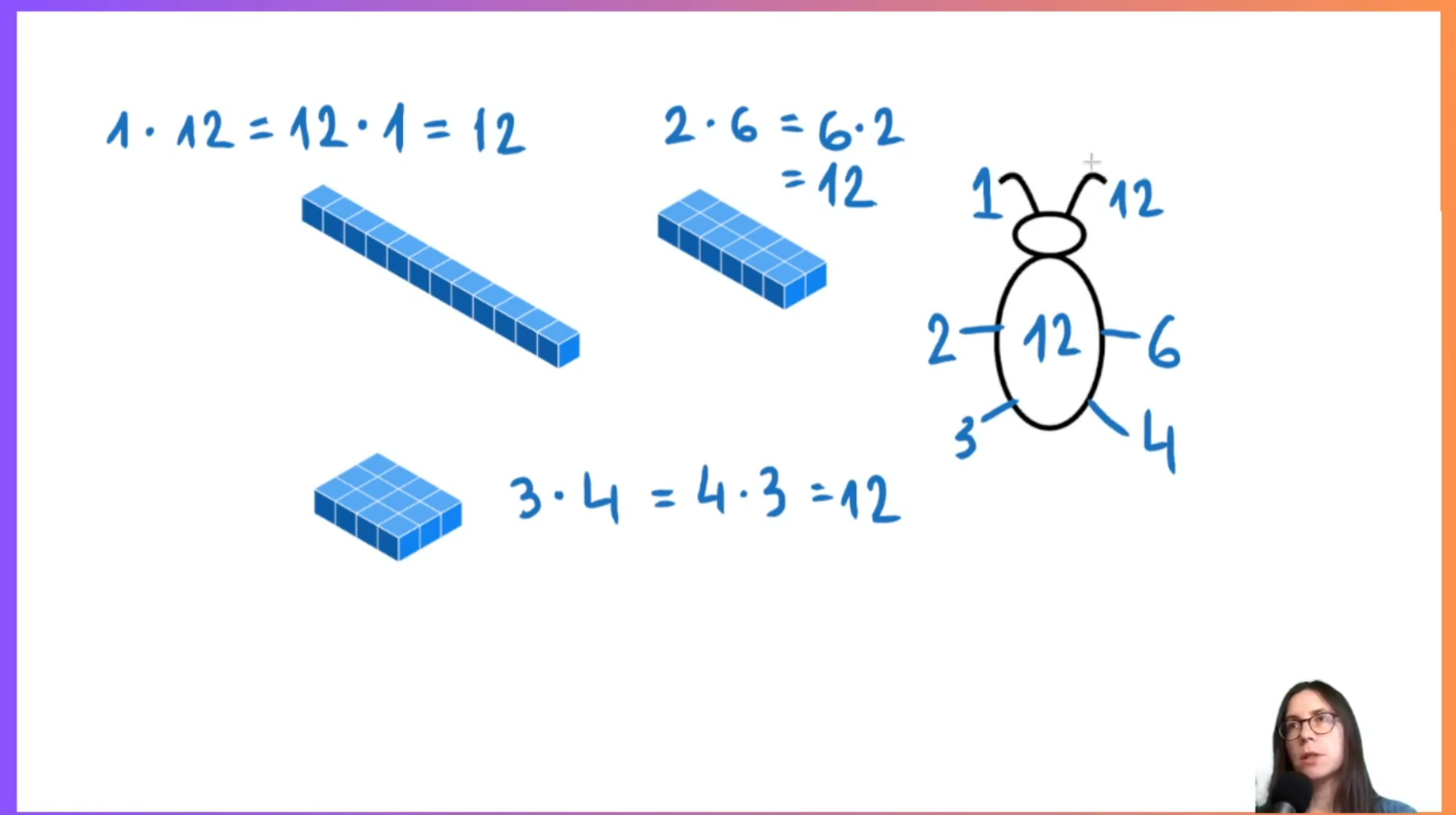
- Liczby pierwsze i złożone: Dziecko nauczy się rozpoznawać te liczby i wizualizować je za pomocą macierzy i pogłębi swoją wiedzę i zrozumienie tematu analizując Sito Eratostenesa.
- Dzielniki i wielokrotności w praktyce (NWD i NWW): Koniec z myleniem dzielnika z wielokrotnością! Wyjaśniamy różnice i pokazujemy, jak wykorzystać te pojęcia do rozwiązywania typowych zadań tekstowych.
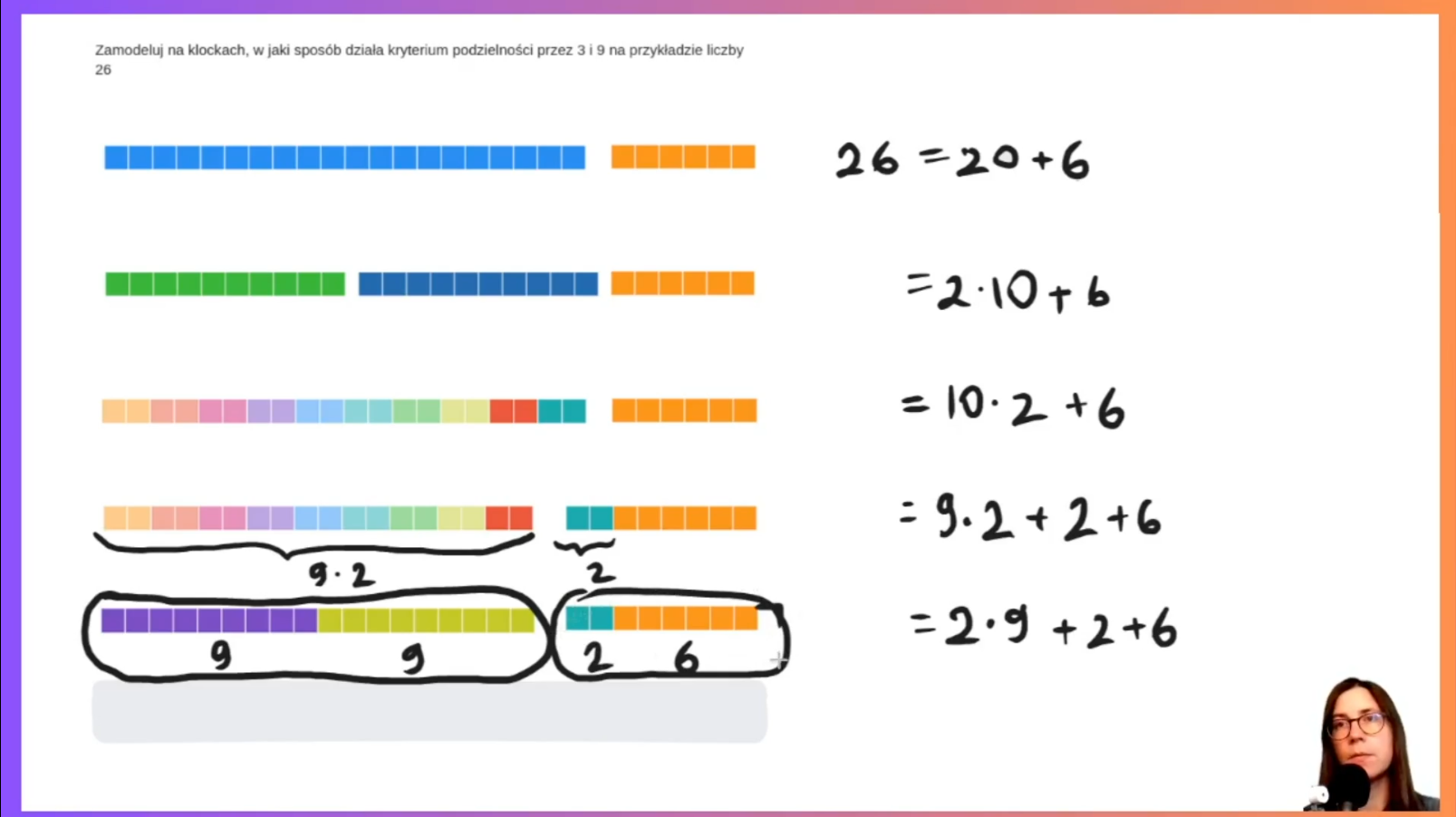
- Kryteria podzielności liczb (2, 3, 4, 5, 8, 9, 10): Uczymy się, jak szybko sprawdzić podzielność liczb bez kalkulatora. Przedstawiamy sens tych reguł (np. skąd bierze się reguła dla 3 i 9), a nie tylko same zasady!
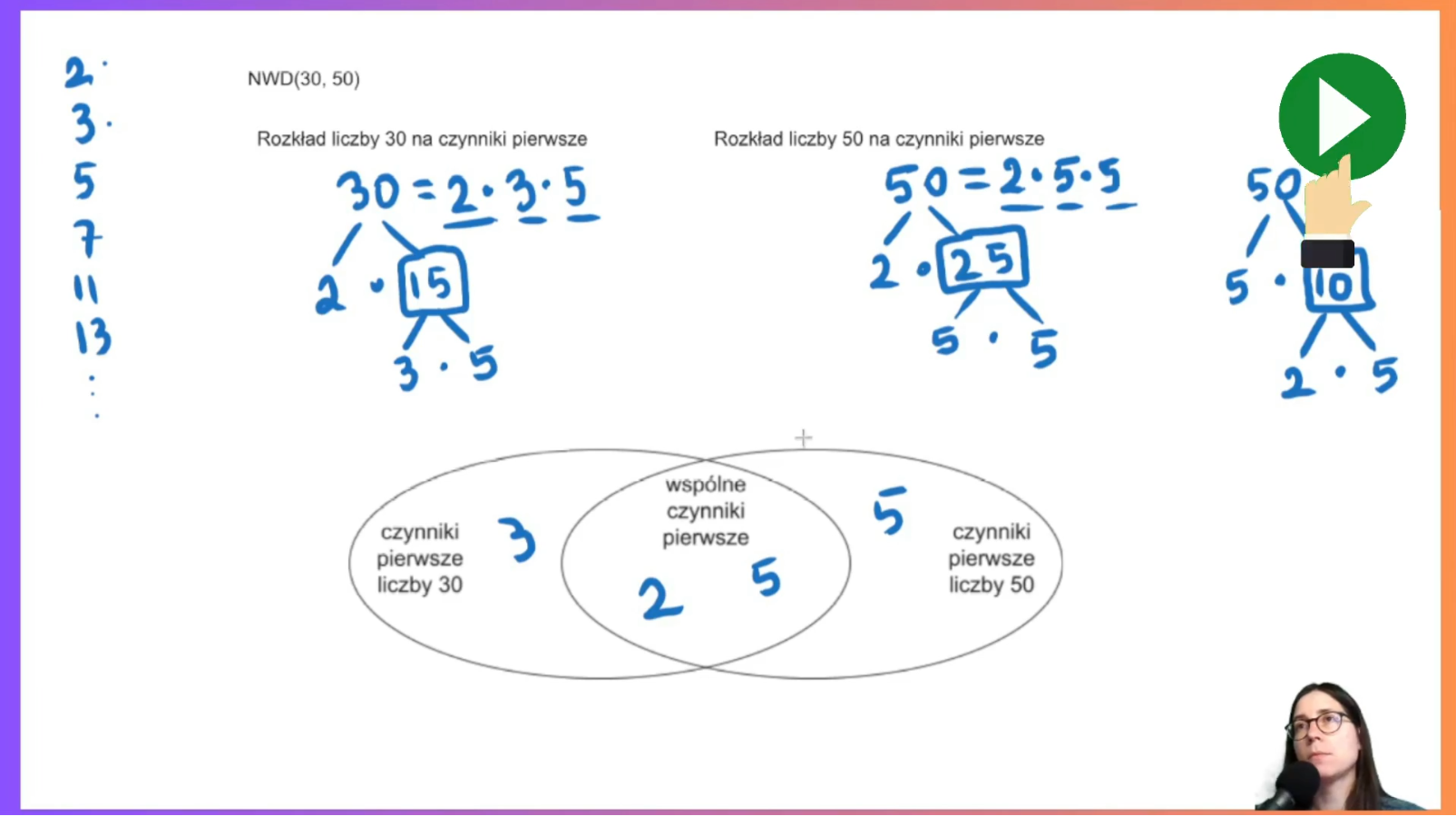
- Rozkład na czynniki pierwsze: Uczymy się budować “drzewka” i wykorzystywać diagramy Venna do obliczania NWD i NWW w oparciu o zrozumienie i bez wkuwania procedur.
- Algorytm Euklidesa: Dziecko pozna ten starożytny algorytm oraz sposób jego wizualizacji w kontekście kafelkowania prostokąta. To najlepszy sposób, aby zrozumieć, w jaki sposób działa ten algorytm i dlaczego otrzymany wynik rzeczywiście jest największym wspólnym dzielnikiem rozpatrywanych liczb!
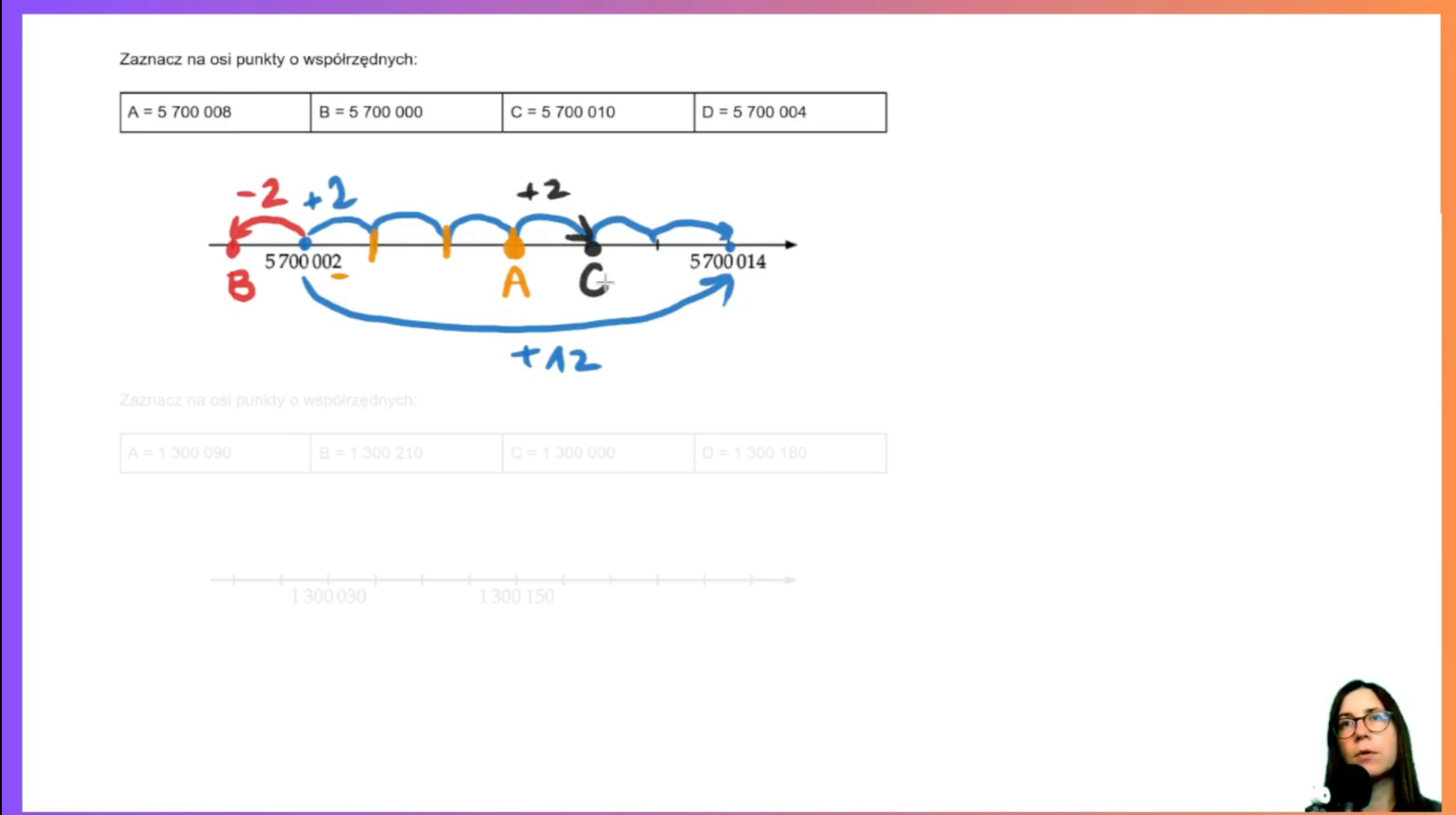
- Odczytywanie i zaznaczanie punktów na osi liczbowej: Przypominamy sobie jak odczytywać współrzędne wskazanego punktu, gdy dane są współrzędne dwóch innych punktów oraz jak zaznaczać na osi punkty o podanych współrzędnych.
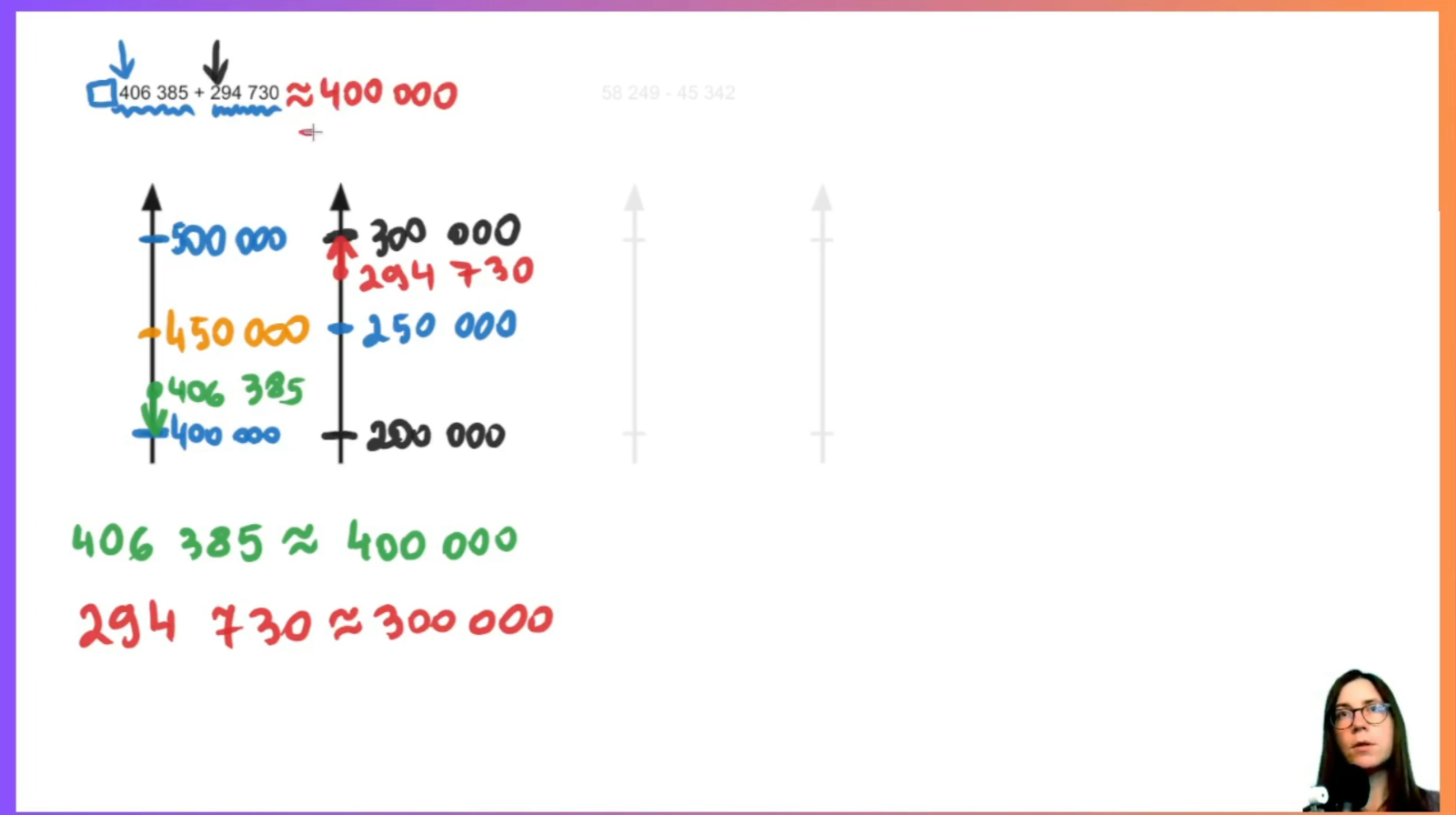
- Zaokrąglanie liczb: Poznajemy zaokrąglanie dużych liczb na osi liczbowej, ucząc się w oparciu o zrozumienie, kiedy zaokrąglać w górę, a kiedy w dół, bez ślepego bazowania na regułce z podręcznika. Uczymy się wykonywać działania przybliżone. Mierzymy się z praktycznymi problemami szacowania liczb, w których nie zawsze należy szacować w sposób oparty o reguły matematyczne.
Dlaczego ten Moduł jest wyjątkowy?
- Podejście wizualne: Zamiast suchych zapisów matematycznych, używamy pomocy wizualnych, aby abstrakcyjne pojęcia stały się namacalne.
- Wzmocnienie logicznego myślenia: Moduł wprowadza zaawansowane myślenie algorytmiczne poprzez wizualne uzasadnienie Algorytmu Euklidesa (kafelkowanie prostokąta). Zamiast nudnej procedury, dziecko widzi, jak działa ,,logiczna machina”, co rozwija umiejętność rozwiązywania problemów na poziomie, który wykracza poza standardowy program
- Matematyka w życiu codziennym: Tematyka NWD i NWW jest natychmiast przenoszona do praktycznych problemów z życia wziętych (pakowanie paczek, spotkania sportowców, cięcie materiału). Dziecko uczy się, że matematyka nie jest oderwana od rzeczywistości, ale jest narzędziem do rozwiązywania realnych dylematów, co zwiększa motywację do nauki.
Potrzebujesz więcej informacji?
Chcesz zobaczyć przykładowe materiały z tego Modułu oraz dokładną listę zagadnień? Zajrzyj tutaj!
Chcesz dowiedzieć się więcej o całym kursie dla piątoklasistów? Zajrzyj tutaj!






P. –
Syn ma orzeczenie i trudności w nauce, ale dzięki kursowi zaczął w końcu rozumieć, dlaczego 17 to liczba pierwsza, a 16 nie. Wcześniej to była dla niego czysta abstrakcja. Czas trwania nagrań jest idealny, syn nie rozprasza się.
Zofia Zielińska-Kolasińska –
Bardzo się cieszę i dziękuję za miły komentarz!
Anka W. –
Dziękuję za ten moduł. Moja córka miała ogromne problemy z NWD i NWW, a dzięki lekcjom w końcu wszystko zrozumiała. Nagrania są świetnie przygotowane, a quizy pomagają na bieżąco sprawdzać wiedzę. Gorąco polecam!
Tata Łucji –
Super!