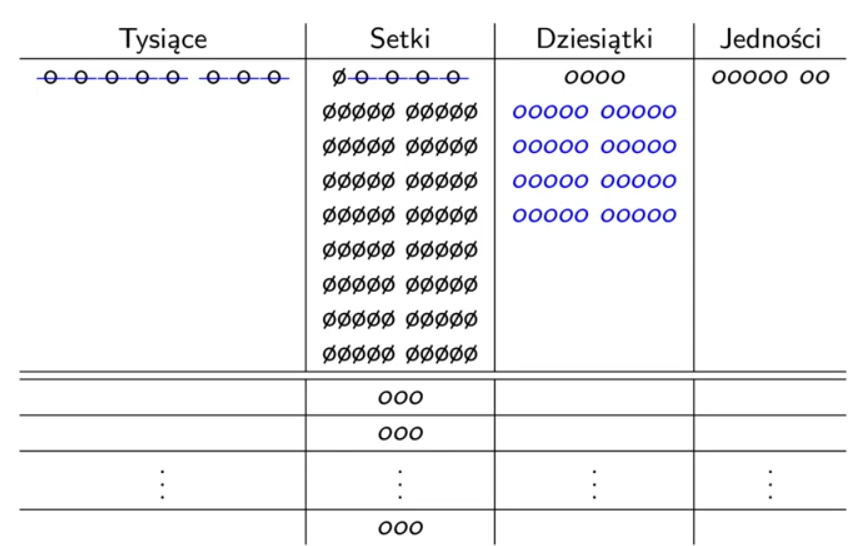
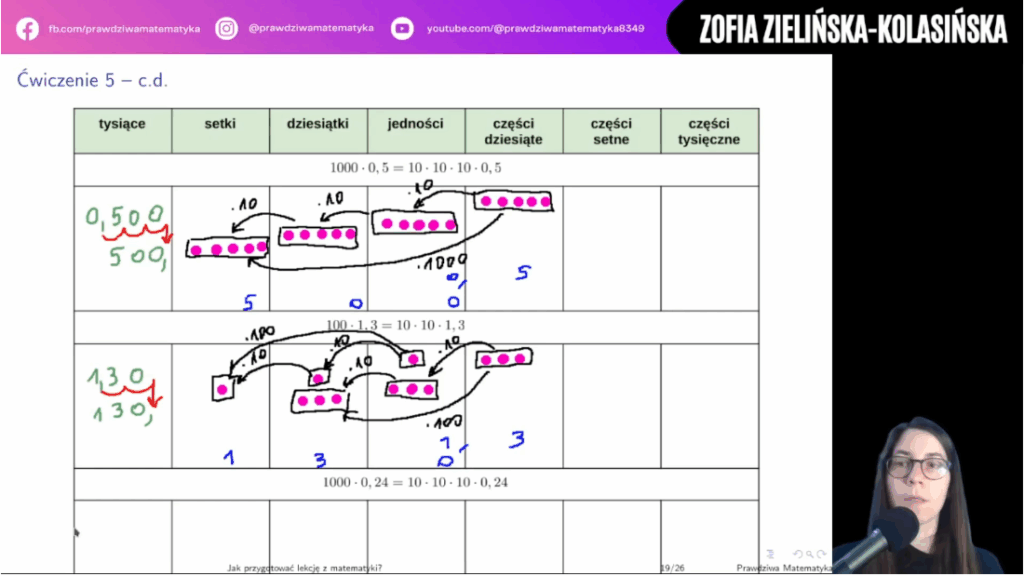
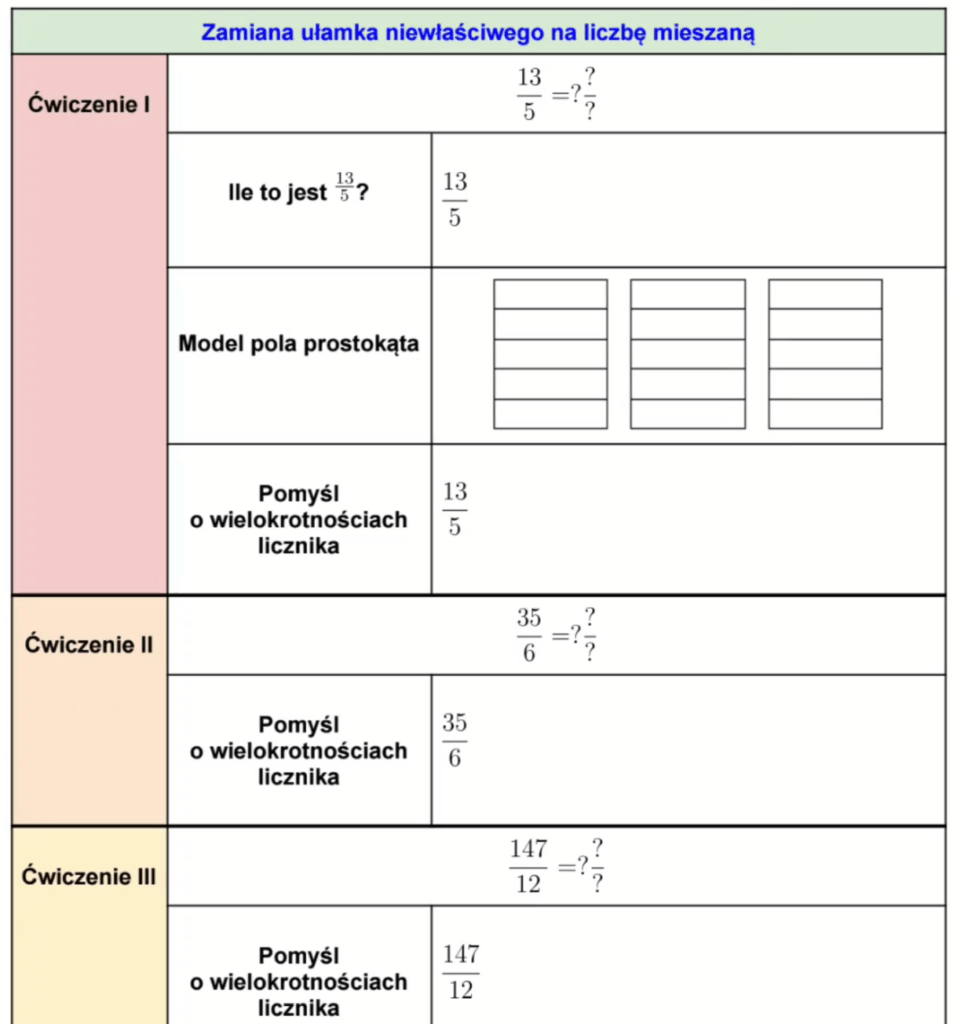
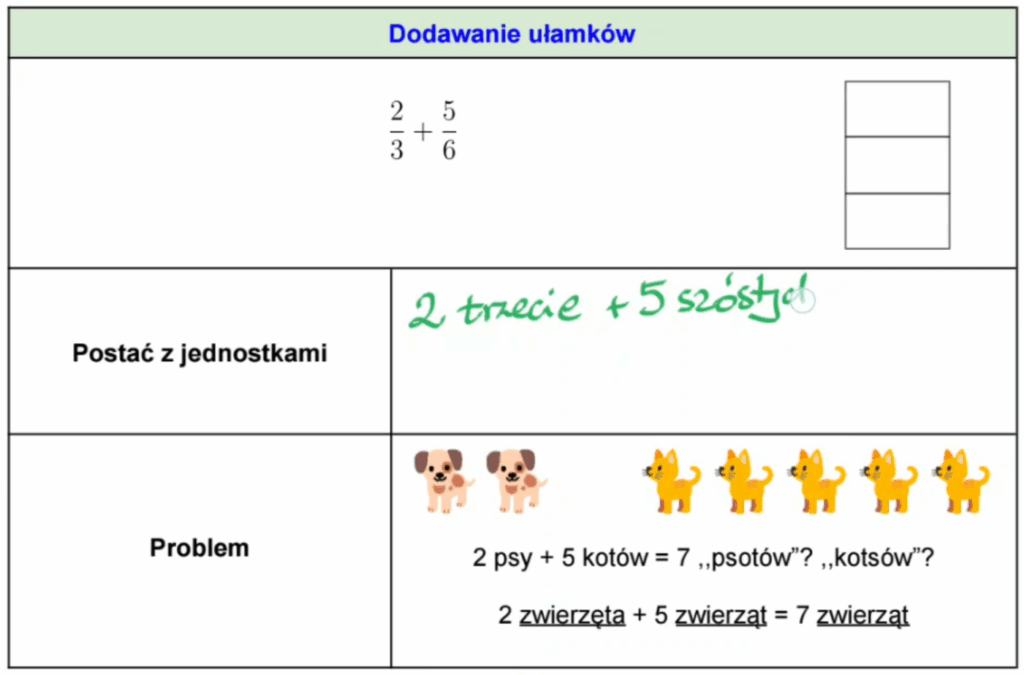
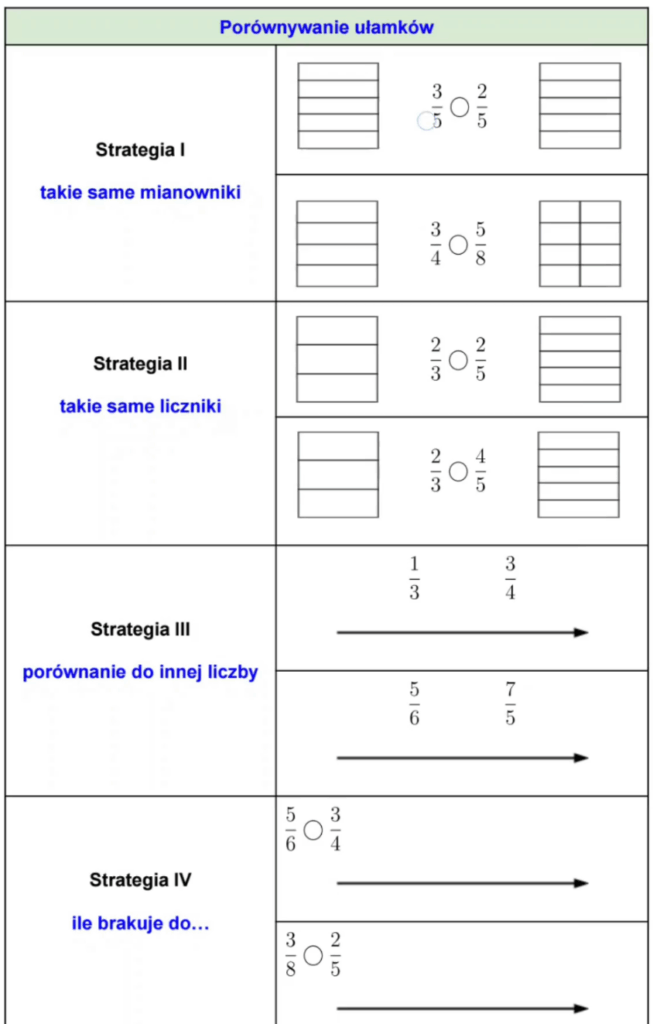
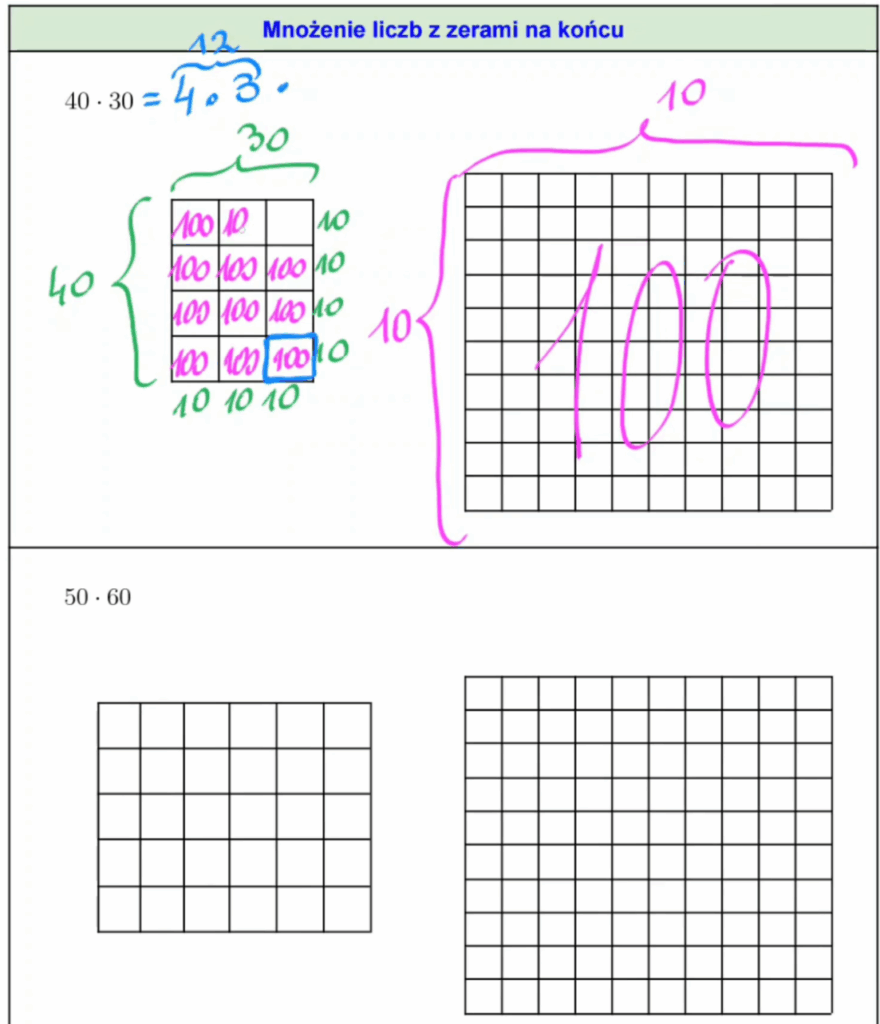
Jak uczyć dodawania i odejmowania ułamków w klasie 3
Witaj! Czy ułamki wydają się Twoim uczniom zbyt abstrakcyjne? Ten wpis to zapis kluczowych myśli z mojego webinaru, w którym pokazałam, jak dodawanie i odejmowanie ułamków o tym samym mianowniku może stać się proste i intuicyjne. Zrozumienie to podstawa – bez niego każda kolejna lekcja staje się trudniejsza, a dzieci zniechęcają się do matematyki. Poniżej […]
Jak uczyć dodawania i odejmowania ułamków w klasie 3 Dowiedz się więcej »